
已知双曲线![]() -
-![]() =1的离心率e>1+
=1的离心率e>1+![]() ,左、右焦点分别为F1,F2,左准线为l,能否在双曲线的左支上找到一点P,使得|PF1|是P到l的距离d与|PF2|的等比中项?
,左、右焦点分别为F1,F2,左准线为l,能否在双曲线的左支上找到一点P,使得|PF1|是P到l的距离d与|PF2|的等比中项?
|
思路 本题为探索性命题,一般可先假设点P存在,再利用已知条件探求,若得出矛盾,则说明P点不存在,否则,便得到P的位置. 解答 设在左半支上存在P点,使|PF1|2=|PF2|·d,由双曲线的第二种定义知 即|PF2|=|PF1|·e, ① 再由双曲线的第一定义,得 |PF2|-|PF1|=2a, ② 由式①、②,解得|PF1|= 因为△PF1F2中有|PF1|+|PF2|≥2c, ∴ 利用e= 解得1- ∵e>1, ∴1<e≤1+ ∴符合条件的点P不存在. 评析 1<e≤1+ |


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
A、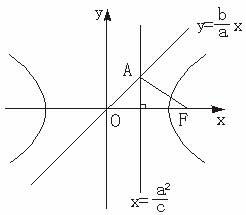
 B、
B、 C、
C、 D、
D、
查看答案和解析>>
科目:高中数学 来源:2014届吉林省高二上学期期末考试理科数学试卷(解析版) 题型:填空题
已知双曲线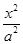 -
-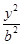 =1(a>0,b>0)的左、右焦点分别为F1、F2,点P在双曲线的右支上,且|PF1|=4|PF2|,则双曲线离心率e的最大值为________.
=1(a>0,b>0)的左、右焦点分别为F1、F2,点P在双曲线的右支上,且|PF1|=4|PF2|,则双曲线离心率e的最大值为________.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省招生仿真卷理科数学试卷(解析版) 题型:选择题
已知双曲线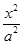 -
-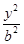 =1(a>0,b>0)的左顶点与抛物线y2=2px(p>0)的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1),则双曲线的焦距为( )
=1(a>0,b>0)的左顶点与抛物线y2=2px(p>0)的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1),则双曲线的焦距为( )
A. 2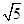 B.2
B.2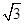 C.4
C.4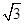 D.4
D.4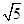
查看答案和解析>>
科目:高中数学 来源:2013届江西省高二下学期第二次月考文科数学试卷(解析版) 题型:解答题
已知双曲线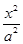 -
- =1(a>0,b>0)的离心率e=
=1(a>0,b>0)的离心率e= ,直线l过A(a,0),B(0,-b)两点,原点O到直线l的距离是
,直线l过A(a,0),B(0,-b)两点,原点O到直线l的距离是 .
.
(1)求双曲线的方程;
(2)过点B作直线m交双曲线于M、N两点,若 ·
· =-23,求直线m的方程.
=-23,求直线m的方程.
查看答案和解析>>
科目:高中数学 来源:2013届安徽省高二下学期期中考试理科数学试卷(解析版) 题型:选择题
已知双曲线-=1(a>0,b>0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是 ( )
A.[1,2] B.(1,2) C.[2,+∞) D.(2,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com