
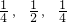 ;
;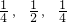 ;
; +
+ =
= .
. ,P(X=30)=
,P(X=30)= ,P(X=50)=
,P(X=50)= ×
× =
= ,
, ×
× =
= ,P(X=90)=
,P(X=90)= ,
,| 候车时间X(分) | 10 | 30 | 50 | 70 | 90 |
| 概率 |  |  |  |  |  |
 +30×
+30× +50×
+50× +70×
+70× +90×
+90× =30.
=30.

科目:高中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西师大附中高三5月模拟考试理科数学试卷(解析版) 题型:解答题
某车站每天上午发出两班客车(每班客车只有一辆车)。第一班客车在8∶00,8∶20,8∶40这三个时刻随机发出,且在8∶00发出的概率为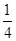 ,8∶20发出的概率为
,8∶20发出的概率为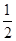 ,8∶40发出的概率为
,8∶40发出的概率为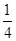 ;第二班客车在9∶00,9∶20,9∶40这三个时刻随机发出,且在9∶00发出的概率为
;第二班客车在9∶00,9∶20,9∶40这三个时刻随机发出,且在9∶00发出的概率为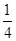 ,9∶20发出的概率为
,9∶20发出的概率为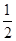 ,9∶40发出的概率为
,9∶40发出的概率为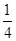 .两班客车发出时刻是相互独立的,一位旅客预计8∶10到站.求:
.两班客车发出时刻是相互独立的,一位旅客预计8∶10到站.求:
(1)请预测旅客乘到第一班客车的概率;
(2)求旅客候车时间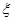 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河北省高三调研理科数学试卷(4) 题型:解答题
某车站每天上午发出两班客车,第一班客车在8∶00,8∶20,8∶40这三个时刻随机发出,且在8∶00发出的概率为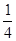 ,8∶20发出的概率为
,8∶20发出的概率为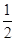 ,8∶40发出的概率为
,8∶40发出的概率为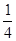 ;第二班客车在9∶00,9∶20,9∶40这三个时刻随机发出,且在9∶00发出的概率为
;第二班客车在9∶00,9∶20,9∶40这三个时刻随机发出,且在9∶00发出的概率为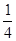 ,9∶20发出的概率为
,9∶20发出的概率为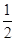 ,9∶40发出的概率为
,9∶40发出的概率为 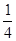 .两班客车发出时刻是相互独立的,一位旅客预计8∶10到站.求:
.两班客车发出时刻是相互独立的,一位旅客预计8∶10到站.求:
(1)请预测旅客乘到第一班客车的概率;
(2)旅客候车时间的分布列;
(3)旅客候车时间的数学期望。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com