Question

已知函数f（x）=x³+mx²+nx-2的图象过点（1，-4），且函数g（x）=f'（x）+6x的图象关于y轴对称．
（1）求m、n的值及函数f（x）的极值；（2）求函数y=f（x）在区间[-2，a]上的最大值．

Answer 1

分析：（Ⅰ）利用条件的到两个关于m、n的方程，求出m、n的值，再找函数y=f（x）的导函数大于0和小于0对应的区间即可．（Ⅱ）利用（Ⅰ）的结论，分①当-2＜a≤0时、②当0＜a≤3时和③当a＞3时，3种情况讨论函数f（x）在区间[-2，a]上和可能的最大值，将函数值加以比较即可得到答案．

解答：解：（Ⅰ）由函数f（x）图象过点（1，-4），得m-n=-3，①
由f（x）=x³+mx²+nx-2，得f′（x）=3x²+2mx+n，
则g（x）=f′（x）+6x=3x²+（2m+6）x+n；
而g（x）图象关于y轴对称，所以-

2m+6

2×3

=0，所以m=-3，
代入①得n=0．所以m、n的值分别为-3、0；
从而f（x）=x³-3x²-2，f′（x）=3x²-6x=3x（x-2）．
由f′（x）＞0得x＞2或x＜0，故f（x）的单调递增区间是（-∞，0），（2，+∞）；
由f′（x）＜0得0＜x＜2，故f（x）的单调递减区间是（0，2）．
∴f（x）的极大值为f（0）=-2，极小值为f（2）=-6；
（Ⅱ）由（Ⅰ）得f′（x）=3x（x-2），
令f′（x）=0得x=0或x=2．
当x变化时，f′（x）、f（x）的变化情况如下表：

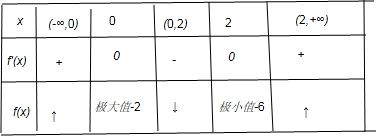
由此可得：
①当-2＜a≤0时，f（x）在[-2，a]内为增函数，最大值为f（a）=a³-3a²-2；
②当0＜a≤3时，由于f（0）≥f（a），f（x）在[-2，a]内最大值为f（0）=-2；
③a＞3时，由于f（0）＜f（a），可得f（x）在[-2，a]内最大值为f（a）=a³-3a²-2．

点评：本小题主要考查函数的奇偶性、单调性、极值、导数、不等式等基础知识，考查运用导数研究函数性质的方法，以及分类与整合、转化与化归等数学思想方法，考查分析问题和解决问题的能力．