
【题目】已知函数![]() ,其中a >2.
,其中a >2.
(I)讨论函数f(x)的单调性;
(II)若对于任意的![]() ,恒有
,恒有![]() ,求a的取值范围.
,求a的取值范围.
(III)设![]() ,
,![]() ,求证:
,求证:![]() .
.
【答案】(1)f(x)的单调递增区间为![]() ,单调减区间为(1,a-1).(2)(2,5];(3)见解析.
,单调减区间为(1,a-1).(2)(2,5];(3)见解析.
【解析】分析:(I)求出![]() ,在定义域内,分别令
,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间,![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;;(II)对任意的
的减区间;;(II)对任意的![]() ,恒有
,恒有![]() ,等价于
,等价于![]() ,令
,令![]() ,即函数
,即函数![]() 在
在![]() 上为增函数,
上为增函数,![]() ,∴
,∴![]() 恒成立,结合基本不等式,即可求实数
恒成立,结合基本不等式,即可求实数![]() 的取值范围;(III) 由(I)可知当
的取值范围;(III) 由(I)可知当![]() 时,函数
时,函数![]() 为减函数,
为减函数,![]() ,由(II)知
,由(II)知![]() ,即可证明结论.
,即可证明结论.
详解:(I)函数f(x)的定义域为![]()
![]()
令![]() ,则
,则![]() ,即
,即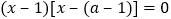
解得![]() 或
或![]() ∵
∵![]() ∴
∴![]()
由![]() ,解得0<x<1或x>a-1,
,解得0<x<1或x>a-1,
由![]() ,解得1<x<a-1
,解得1<x<a-1
∴函数f(x)的单调递增区间为![]() ,单调减区间为(1,a-1).
,单调减区间为(1,a-1).
(II)设![]() ,则不等式
,则不等式![]() 等价于
等价于![]() ·
·
整理得,![]()
令![]()
∴函数g(x)在x∈(0,+∞)上为增函数.
∵![]() ,∴
,∴![]() 恒成立
恒成立
而![]()
∴![]() ∵a>2 ∴
∵a>2 ∴![]()
∴![]() ,即a的取值范围是(2,5].
,即a的取值范围是(2,5].
(III)∵![]() 由(I)可知当
由(I)可知当![]() 时,函数f(x)为减函数,
时,函数f(x)为减函数,
而![]()
那么![]() ∴
∴ ![]()
由(II)知![]()
∴![]()
即![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() ,点
,点![]() ,
,![]() 是圆上一动点,点
是圆上一动点,点![]() 在线段
在线段![]() 上,点
上,点![]() 在半径
在半径![]() 上,且满足
上,且满足![]() .
.
(1)当![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与轨迹
与轨迹![]() 交于点
交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线交
的直线交![]() 于点
于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,求点
,求点![]() 横坐标的取值范围.
横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,当直线
两点,当直线![]() 过点
过点![]() 时,以
时,以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.
(1)求抛物线![]() 的方程;
的方程;
(2)与![]() 平行的直线
平行的直线![]() 交抛物线于
交抛物线于![]() ,
,![]() 两点,若平行线
两点,若平行线![]() ,
,![]() 之间的距离为
之间的距离为![]() ,且
,且![]() 的面积是
的面积是![]() 面积的
面积的![]() 倍,求
倍,求![]() 和
和![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆C:![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,上顶点为A,在x轴负半轴上有一点B,满足
,上顶点为A,在x轴负半轴上有一点B,满足![]() 为线段
为线段![]() 的中点,且AB⊥
的中点,且AB⊥![]() 。
。
(I)求椭圆C的离心率;
(II)若过A、B、![]() 三点的圆与直线
三点的圆与直线![]() :
:![]() 相切,求椭圆C的方程;
相切,求椭圆C的方程;
(III)在(I)的条件下,过右焦点![]() 作斜率为k的直线与椭圆C交于M,N两点,在x轴上是否存在点P(m,0)使得以PM,PN为邻边的平行四边形是菱形?如果存在,求出m的取值范围;如果不存在,说明理由。
作斜率为k的直线与椭圆C交于M,N两点,在x轴上是否存在点P(m,0)使得以PM,PN为邻边的平行四边形是菱形?如果存在,求出m的取值范围;如果不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司共有60位员工,为提高员工的业务技术水平,公司拟聘请专业培训机构进行培训.培训的总费用由两部分组成:一部分是给每位参加员工支付400元的培训材料费;另一部分是给培训机构缴纳的培训费.若参加培训的员工人数不超过30人,则每人收取培训费1000元;若参加培训的员工人数超过30人,则每超过1人,人均培训费减少20元.设公司参加培训的员工人数为x人,此次培训的总费用为y元.
(1)求出y与x之间的函数关系式;
(2)请你预算:公司此次培训的总费用最多需要多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
某建筑公司用8000万元购得一块空地,计划在该地块上建造一栋至少12层、每层4000平方米的楼房.经初步估计得知,如果将楼房建为x(x![]() 12)层,则每平方米的平均建筑费用为Q(x)=3000+50x(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?每平方米的平均综合费最小值是多少?
12)层,则每平方米的平均建筑费用为Q(x)=3000+50x(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?每平方米的平均综合费最小值是多少?
(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用=![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌汽车的![]() 店,对最近100份分期付款购车情况进行统计,统计情况如下表所示.已知分9期付款的频率为0.4;该店经销一辆该品牌汽车,若顾客分3期付款,其利润为1万元;分6期或9期付款,其利润为2万元;分12期付款,其利润为3万元.
店,对最近100份分期付款购车情况进行统计,统计情况如下表所示.已知分9期付款的频率为0.4;该店经销一辆该品牌汽车,若顾客分3期付款,其利润为1万元;分6期或9期付款,其利润为2万元;分12期付款,其利润为3万元.
付款方式 | 分3期 | 分6期 | 分9期 | 分12期 |
频数 | 20 | 20 |
|
|
(1)若以上表计算出的频率近似替代概率,从该店采用分期付款购车的顾客(数量较大)中随机抽取3为顾客,求事件![]() :“至多有1位采用分6期付款“的概率
:“至多有1位采用分6期付款“的概率![]() ;
;
(2)按分层抽样方式从这100为顾客中抽取5人,再从抽取的5人中随机抽取3人,记该店在这3人身上赚取的总利润为随机变量![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com