
【题目】函数![]() 在R上为偶函数且在
在R上为偶函数且在![]() 单调递减,若
单调递减,若![]() 时,不等式
时,不等式![]() 恒成立,则实数m的取值范围为( )
恒成立,则实数m的取值范围为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】B
【解析】
根据函数的奇偶性和单调性将不等式进行转化,利用参数分离法,结合函数的最值,利用导数求得相应的最大值和最小值,从而求得m的范围.
∵函数f(x)为偶函数,
若不等式f(2mx﹣lnx﹣3)≥2f(3)﹣f(﹣2mx+lnx+3)对x∈[1,3]恒成立,
等价为f(2mx﹣lnx﹣3)≥2f(3)﹣f(2mx﹣lnx﹣3)
即2f(2mx﹣lnx﹣3)≥2f(3)对x∈[1,3]恒成立.
即f(2mx﹣lnx﹣3)≥f(3)对x∈[1,3]恒成立.
∵f(x)在[0,+∞)单调递减,
∴﹣3≤2mx﹣lnx﹣3≤3对x∈[1,3]恒成立,
即0≤2mx﹣lnx≤6对x∈[1,3]恒成立,
即2m![]() 且2m
且2m![]() 对x∈[1,3]恒成立.
对x∈[1,3]恒成立.
令g(x)![]() ,则g′(x)
,则g′(x)![]() ,在[1,e]上递增,在[e,3]上递减,则g(x)的最大值为g(e)
,在[1,e]上递增,在[e,3]上递减,则g(x)的最大值为g(e)![]() ,
,
h(x)![]() ,则h′(x)
,则h′(x)![]() 0,则函数h(x)在[1,3]上递减,则h(x)的最小值为h(3)
0,则函数h(x)在[1,3]上递减,则h(x)的最小值为h(3)![]() ,
,
则 ,得
,得 ,即
,即![]() m
m![]() ,
,
故选:B.


科目:高中数学 来源: 题型:
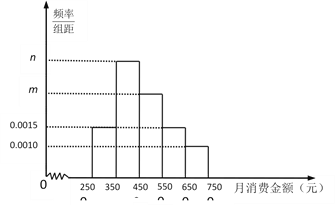
【题目】某机构为了解某地区中学生在校月消费情况,随机抽取了100名中学生进行调查.右图是根据调查的结果绘制的学生在校月消费金额的频率分布直方图.已知[350,450),[450,550),[550,650)三个金额段的学生人数成等差数列,将月消费金额不低于550元的学生称为“高消费群” .
(1)求m,n的值,并求这100名学生月消费金额的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)根据已知条件完成下面2×2列联表,并判断能否有90%的把握认为“高消费群”与性别有关?
高消费群 | 非高消费群 | 合计 | |
男 | |||
女 | 10 | 50 | |
合计 |
(参考公式:![]() ,其中
,其中![]() )
)
P( | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市![]() 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.

(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取![]() 户居民,则月平均用电量在
户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网购是当前民众购物的新方式,某公司为改进营销方式,随机调査了100名市民,统计其周平均网购
的次数,并整理得到如右的频数直方图,将周平均网购次数不小于4次的民众称为网购迷.这100名市民中,年龄不超过40岁的有65人,且网购迷中有5名市民的年龄超过40岁
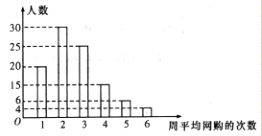
(1)根据已知条件完成下面的2×2列联表,能否在犯错误的概率不超过0.10的前提条件下认为网购迷与年龄不超过40岁有关?

(2)现从网购迷中按分层抽样选5人代表进一步进行调查,若从5人代表中任意挑选2人,求挑选的2人中有年龄超过40岁的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,短轴长为
,短轴长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() 是椭圆
是椭圆![]() 的上焦点.问:是否存在直线
的上焦点.问:是否存在直线![]() ,使得
,使得![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司共有10条产品生产线,不超过5条生产线正常工作时,每条生产线每天纯利润为1100元,超过5条生产线正确工作时,超过的生产线每条纯利润为800元,原生产线利润保持不变.未开工的生产线每条每天的保养等各种费用共100元.用x表示每天正常工作的生产线条数,用y表示公司每天的纯利润.
(I)写出y关于x的函数关系式,并求出纯利润为7700元时工作的生产线条数.
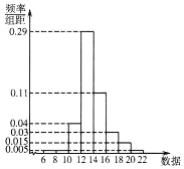
(II)为保证新开的生产线正常工作,需对新开的生产线进行检测,现从该生产线上随机抽取100件产品,测量产品数据,用统计方法得到样本的平均数![]() ,标准差
,标准差![]() ,绘制如图所示的频率分布直方图,以频率值作为概率估计值.为检测该生产线生产状况,现从加工的产品中任意抽取一件,记其数据为X,依据以下不等式评判(P表示对应事件的概率)
,绘制如图所示的频率分布直方图,以频率值作为概率估计值.为检测该生产线生产状况,现从加工的产品中任意抽取一件,记其数据为X,依据以下不等式评判(P表示对应事件的概率)
①![]()
②![]()
③![]()
评判规则为:若至少满足以上两个不等式,则生产状况为优,无需检修;否则需检修生产线.试判断该生产线是否需要检修.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一工厂生产了某种产品700件,该工厂需要对这些产品的性能进行检测现决定利用随机数表法从中抽取100件产品进行抽样检测,将700件产品按001,002,…,700进行编号
(1)如果从第8行第4列的数开始向右读,请你依次写出最先检测的3件产品的编号;(下面摘取了随机数表的第7~9行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
(2)检测结果分为优等、合格、不合格三个等级,抽取的100件产品的安全性能和环保性能的检测结果如下表(横向和纵向分别表示安全性能和环保性能):
(i)若在该样本中,产品环保性能是优等的概率为34%,求![]() 的值;
的值;
(ii)若![]() ,求在安全性能不合格的产品中,环保性能为优等的件数比不合格的件数少的概率.
,求在安全性能不合格的产品中,环保性能为优等的件数比不合格的件数少的概率.
件数 | 环保性能 | |||
优等 | 合格 | 不合格 | ||
安全性能 | 优等 | 6 | 20 | 5 |
合格 | 10 | 18 | 6 | |
不合格 | m | 4 | n | |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com