
����Ŀ��ʮ�Ŵ�������ijƶ��������ƶ������᳹��ʵ���Ҿ���ƶ������Ҫ������ũ���������Ⱥ����ƶ��С����������и�ķ���ƴ������ũ�彨��ȡ�þ������ũ��������Ҳ�������ӡ�Ϊ�˸��õ��ƶ�2019����ڼӿ�����ũ������������������ƶ�Ĺ����ƻ����õط�ƶ��ͳ����2018��50λũ��������˲��Ƴ�����Ƶ�ʷֲ�ֱ��ͼ��
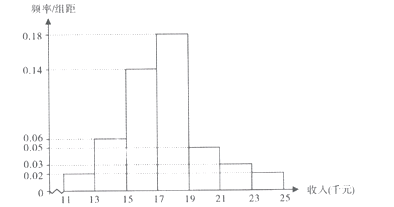
��1������Ƶ�ʷֲ�ֱ��ͼ������50λũ�����ƽ������![]() ����λ��ǧԪ����ͬһ�������ø�������������е�ֵ��ʾ����
����λ��ǧԪ����ͬһ�������ø�������������е�ֵ��ʾ����
��2����Ƶ�ʷֲ�ֱ��ͼ��������Ϊ��ƶ������ũ��������![]() ������̬�ֲ�
������̬�ֲ�![]() ������
������![]() ����Ϊ��ƽ������
����Ϊ��ƽ������![]() ,
,![]() ������������
������������![]() ���������
���������![]() .���ø���̬�ֲ�����:
.���ø���̬�ֲ�����:
(i)��2019����ƶ���Ṥ���У���ʹ�õ���Լ��ռ��ũ��������![]() ��ũ�����������ڷ�ƶ���ƶ���������������������������ԼΪ����ǧԪ��
��ũ�����������ڷ�ƶ���ƶ���������������������������ԼΪ����ǧԪ��
��ii��Ϊ�˵��С�����ƶ������һ�ˡ�������Ҫ����ʵ���, ��ƶ������߷���1000λũ����ÿ��ũ�����������������ʣ���1000λũ���е������벻����12.14ǧԪ���������п����Ƕ��٣�
�����ο������빫ʽ![]() ����
����![]() ��
��![]() �����
�����![]() ����
����![]() ����
����![]() .
.
���𰸡�(1)17.40��Ԫ (2) (i) 14.77ǧԪ ��ii��978
��������
��1����ÿһ��С�����е�ĺ��������Ƶ�����͵ô𰸣�
��2�������⣬X��N��17.40��6.92������
��i������֪�������P��x�������ң�����һ����������ҵô𰸣�
���������P��X��12.14������ÿ��ũ�������벻����12.14ǧԪ���¼�����Ϊ0.9773����1000��ũ�������벻����12.14ǧԪ������Ϊ����������B��103��p�������ǡ����k��ũ��������벻����12.14ǧԪ���¼����ʣ���![]() 1����k��1001p�����1001p��978.233����k��������ô𰸣�
1����k��1001p�����1001p��978.233����k��������ô𰸣�
�⣺��1��![]() ǧԪ.
ǧԪ.
��2�������⣬![]() ��
��![]() .
.
��i��![]()
![]() ʱ����������
ʱ����������
������������ԼΪ14.77ǧԪ
��ii����![]() ����
����
ÿ��ũ��������벻����12.14ǧԪ���¼�����Ϊ0.9773��
��1000��ũ��������벻����12.14ǧԪ������Ϊ![]() ����
����![]() ������
������![]() ��
��
����ǡ����![]() ��ũ��������벻����12.14ǧԪ���¼�������
��ũ��������벻����12.14ǧԪ���¼�������![]()
�Ӷ���![]() ����
����![]()
��![]() �����ԣ�
�����ԣ�
��![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
�ɴ˿�֪�������߷õ�1000λũ���У������벻����12.14ǧԪ���������п�����978



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4������ϵ���������
��ƽ��ֱ������ϵ![]() �У�Բ
�У�Բ![]() ��
��![]() ��ֱ��
��ֱ��![]() ��
��![]() ��ֱ��
��ֱ��![]() ����
����![]() ����б��Ϊ
����б��Ϊ![]() ����ԭ��
����ԭ��![]() Ϊ���㣬
Ϊ���㣬![]() ���������Ϊ���Ὠ��������ϵ.
���������Ϊ���Ὠ��������ϵ.
��1��д��ֱ��![]() ��Բ
��Բ![]() �Ľ��㼫���꼰ֱ��
�Ľ��㼫���꼰ֱ��![]() �IJ������̣�
�IJ������̣�
��2����ֱ��![]() ��Բ
��Բ![]() ����
����![]() ��
��![]() ���㣬��
���㣬��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() .
.
��1���������![]() ��
��![]() ��������ʵ��
��������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����![]() ��֤����
��֤����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������![]() �У�
�У�![]() �����Ϊ
�����Ϊ![]() ��
��![]() .��
.��![]() Ϊ�߶�
Ϊ�߶�![]() ���е�.
���е�.
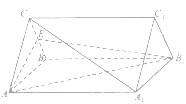
��1�����߶�![]() ����һ��
����һ��![]() ��ʹ��ƽ��
��ʹ��ƽ��![]() ƽ��
ƽ��![]() ����֤����
����֤����
��2��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
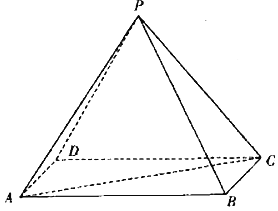
����Ŀ����ͼ��������P-ABCD�У�����ABCD��ƽ���ı��Σ�AB=2AD=2����DAB=60����PA=PC=2����ƽ��ACP��ƽ��ABCD��
������֤��CB��PD��
����������C-PB-A������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() �����ҽ���ֱ�Ϊ
�����ҽ���ֱ�Ϊ![]() ��
��![]() ��
��![]() Ϊ��Բ�ϲ������Ҷ����غϵ�����һ�㣬
Ϊ��Բ�ϲ������Ҷ����غϵ�����һ�㣬![]() ��
��![]() �ֱ�Ϊ
�ֱ�Ϊ![]() �����ġ����ģ���
�����ġ����ģ���![]() ��ʱ����Բ��������Ϊ( )
��ʱ����Բ��������Ϊ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Ա�ڶ�����֬������������֮���ϵ���о��У������һЩ�����֬�������ļ�����������ݣ����±���

�����ϱ������ݵõ����µ�ɢ��ͼ��
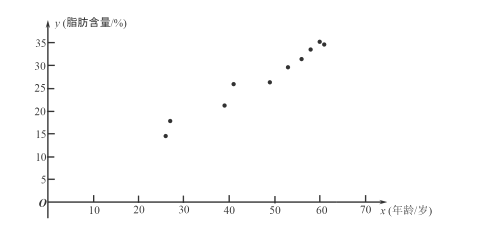
(1)�����ϱ��е��������ݼ���ɢ��ͼ��
(i)��![]() ;
;
(ii)�����������ϵ������ȷ��0.01�������̻����ǵ���س̶ȣ�
(2)��y����x�����Իع鷽��Ϊ![]() ����
����![]() ��ֵ����ȷ��0.01���������ݻع鷽�̹�������Ϊ50��ʱ�����֬��������
��ֵ����ȷ��0.01���������ݻع鷽�̹�������Ϊ50��ʱ�����֬��������
�����ο����ݣ�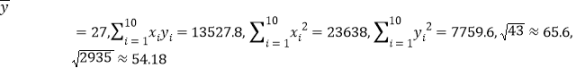
�ο���ʽ�����ϵ��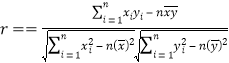
�ع鷽��![]() ��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ
��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ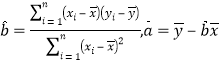
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��
��![]() �������ҽ���ֱ�Ϊ
�������ҽ���ֱ�Ϊ![]() ��
��![]() ����Ϊ
����Ϊ![]() ��������Ϊ
��������Ϊ![]() ����
����![]() ����Բ�ϵĶ��㣬
����Բ�ϵĶ��㣬![]() ����������ֵΪ
����������ֵΪ![]() .
.
(1)����Բ![]() �ķ��̣�
�ķ��̣�
(2)�辭����![]() ��ֱ��
��ֱ��![]() ����Բ
����Բ![]() �ཻ�ڲ�ͬ������
�ཻ�ڲ�ͬ������![]() ��
��![]() ���߶�
���߶�![]() ���д���Ϊ
���д���Ϊ![]() .��ֱ��
.��ֱ��![]() ��ֱ��
��ֱ��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����ֱ��
����ֱ��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����
����![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���¸�˰����2019��1��1�ս���ʵʩ.Ϊ�˵������Ա�����¸�˰��������̶ȣ��о���Ա��![]() �ظ��������������ȡ��1000��Ա�����е��飬��������̶��Է�������ʽͳ�Ƴ����µ�Ƶ�ʷֲ�ֱ��ͼ������
�ظ��������������ȡ��1000��Ա�����е��飬��������̶��Է�������ʽͳ�Ƴ����µ�Ƶ�ʷֲ�ֱ��ͼ������![]() .
.
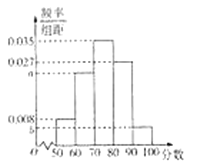
�����Ʊ������Ա��������̶ȵ���λ������������������λС����
���������շֲ������![]() ��
��![]() �������ȡ8�ˣ��ٴ���8���������ȡ4�ˣ��Ƿ�����
�������ȡ8�ˣ��ٴ���8���������ȡ4�ˣ��Ƿ�����![]() ������Ϊ
������Ϊ![]() ����
����![]() �ķֲ�������ѧ������
�ķֲ�������ѧ������
������Ƶ�ʹ��Ƹ��ʣ������о���Ա��ȫ������Ա���������ȡ![]() �������飬�dzɼ���
�������飬�dzɼ���![]() ��
��![]() ������Ϊ
������Ϊ![]() ����
����![]() ����
����![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com