
分析 (Ⅰ)根据二次函数的性质求出函数在(-4,1)的值域即可;
(Ⅱ)通过讨论k的范围,集合二次函数的性质,确定k的范围即可;
(Ⅲ)通过讨论k的范围,判断函数的单调性,从而确定k的范围即可.
解答 解:(Ⅰ)当k=4时,f(x)=2x2+8x-3=2(x+2)2-11,
f(x)的对称轴是x=-2,f(x)在(-4,-2)递减,在(-2,1)递增,
所以f(x)min=f(2)=-11,f(x)max=f(1)=7,
所以f(x)的值域为[-11,7)-----------------------(3分)
(Ⅱ)若函数f(x)在(0,+∞)上至少有一个零点,可分为以下三种情况:
①若k-2>0即k>2时,f(x)=(k-2)x2+2kx-3的对称轴方程为$x=\frac{k}{2-k}<0$,
又f(0)=-3<0,由图象可知f(x)在(0,+∞)上必有一个零点;----------------------(4分)
②若k-2=0即k=2时,f(x)=4x-3,令f(x)=0得$x=\frac{3}{4}>0$,
知f(x)在(0,+∞)上必有一个零点$\frac{3}{4}$;----------------------(5分)
③若k-2<0即k<2时,要使函数f(x)在(0,+∞)上至少有一个零点,
则需要满足$\left\{{\begin{array}{l}{x=\frac{2k}{2-k}>0}\\{△=4{k^2}+12(k-2)≥0}\end{array}}\right.$解得$\left\{{\begin{array}{l}{0<k<2}\\{k≥\frac{{-3+\sqrt{33}}}{2}或k≤\frac{{-3-\sqrt{33}}}{2}}\end{array}}\right.$,
所以$\frac{{-3+\sqrt{33}}}{2}≤k<2$--------------------(7分)
综上可知,若函数f(x)在(0,+∞)上至少有一个零点,k的取值范围为$[\frac{{-3+\sqrt{33}}}{2},+∞)$----------------------(8分)
( III)①当k=2时,f(x)=4x-3在区间[1,2]上单增,所以k=2成立;-------(9分)
②当k>2时,∵f(0)=-3<0,显然在f(x)在区间[1,2]上单增,所以k>2也成立;
--------------------(10分)
③当k<2时,∵f(0)=-3,∴必有$\frac{k}{2-k}≥2$成立,解得$\frac{4}{3}≤k<2$.---------------(11分)
综上k的取值范围为$[\frac{4}{3},+∞)$----------------------(12分)
点评 本题考查了函数的单调性、最值问题,考查二次函数的性质以及分类讨论思想,是一道中档题.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:解答题
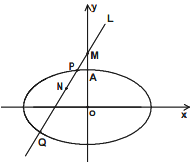 如图,已知椭圆的中心在坐标原点,焦点在x轴上,它的一个顶点为A(0,$\sqrt{2}$),且离心率等于$\frac{{\sqrt{3}}}{2}$,过点M(0,2)的直线l与椭圆相交于不同两点P,Q,点N在线段PQ上.
如图,已知椭圆的中心在坐标原点,焦点在x轴上,它的一个顶点为A(0,$\sqrt{2}$),且离心率等于$\frac{{\sqrt{3}}}{2}$,过点M(0,2)的直线l与椭圆相交于不同两点P,Q,点N在线段PQ上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (0,$\frac{1}{2}$)∪(2,+∞) | C. | (0,$\frac{1}{8}$)∪($\frac{1}{2}$,2) | D. | (0,$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{5}\sqrt{5}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\frac{4}{5}\sqrt{5}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 求1+2+3+…+10的和 | B. | 解方程组$\left\{\begin{array}{l}{x+y+5=0}\\{x-y+3=0}\end{array}\right.$ | ||
| C. | 求半径为3的圆的面积 | D. | 判断y=x2在R上的单调性 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (7,-6) | B. | (7,6) | C. | (6,7) | D. | (-7,6) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 宏利重工有限公司从2012年起,若不改善生产环境,按现状生产,每月收入为70万元,同时将受到环保部门的处罚,第一个月罚3万元,以后每月递增2万元的处罚.如果从2012年一月起投资400万元增加回收净化设备以改善生产环境(改造设备时间不计).按测算,新设备投产后的月收入与时间的关系如图所示.
宏利重工有限公司从2012年起,若不改善生产环境,按现状生产,每月收入为70万元,同时将受到环保部门的处罚,第一个月罚3万元,以后每月递增2万元的处罚.如果从2012年一月起投资400万元增加回收净化设备以改善生产环境(改造设备时间不计).按测算,新设备投产后的月收入与时间的关系如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com