
【题目】为了解某地中小学生的近视形成原因,教育部门委托医疗机构对该地所有中小学生的视力做了一次普查.现该地中小学生人数和普查得到的近视情况分别如图1和图2所示.
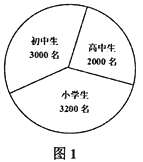
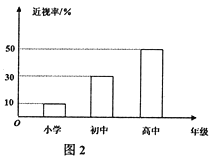
(1)求该地中小学生的平均近视率(保留两位有效数字);
(2)为调查中学生用眼卫生习惯,该地用分层抽样的方法从所有初中生和高中生中确定5人进行问卷调查,再从这5人中随机选取2人继续访谈,则此2人全部来自高中年级的概率是多少?
科目:高中数学 来源: 题型:
【题目】近年,国家逐步推行全新的高考制度.新高考不再分文理科,某省采用3+3模式,其中语文、数学、外语三科为必考科目,满分各150分,另外考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物6门科目中自选3门参加考试(6选3),每科目满分100分.为了应对新高考,某高中从高一年级1000名学生(其中男生550人,女生450人)中,采用分层抽样的方法从中抽取![]() 名学生进行调查.
名学生进行调查.
(1)已知抽取的![]() 名学生中含男生55人,求
名学生中含男生55人,求![]() 的值;
的值;
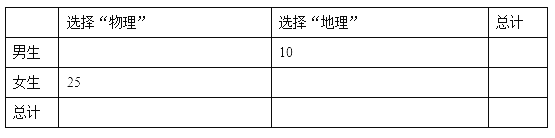
(2)学校计划在高一上学期开设选修中的“物理”和“地理”两个科目,为了了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的![]() 名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),下表是根据调查结果得到的
名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),下表是根据调查结果得到的![]() 列联表. 请将列联表补充完整,并判断是否有 99%的把握认为选择科目与性别有关?说明你的理由;
列联表. 请将列联表补充完整,并判断是否有 99%的把握认为选择科目与性别有关?说明你的理由;
(3)在抽取到的女生中按(2)中的选课情况进行分层抽样,从中抽出9名女生,再从这9名女生中抽取4人,设这4人中选择“地理”的人数为![]() ,求
,求![]() 的分布列及期望.
的分布列及期望.
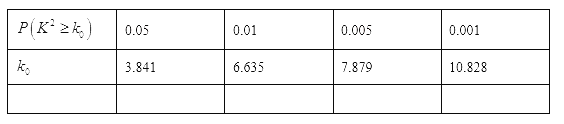
附:![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且其离心率为
,且其离心率为![]() ,过坐标原点
,过坐标原点![]() 作两条互相垂直的射线与椭圆
作两条互相垂直的射线与椭圆![]() 分别相交于
分别相交于![]() ,
,![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在圆心在原点的定圆与直线![]() 总相切?若存在,求定圆的方程;若不存在,请说明理由.
总相切?若存在,求定圆的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且2ccosB=2a+b.
(1)求角C的大小;
(2)若△ABC的面积等于![]() ,求ab的最小值.
,求ab的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱中![]() ,它的体积是
,它的体积是![]() 底面△ABC中,∠BAC=90°,AB=4,AC=3,
底面△ABC中,∠BAC=90°,AB=4,AC=3,![]() 在底面的射影是D,且D为BC的中点.
在底面的射影是D,且D为BC的中点.
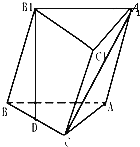
(1)求侧棱![]() 与底面ABC所成角的大小;
与底面ABC所成角的大小;
(2)求异面直线![]() 与
与![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】手机运动计步已成为一种时尚,某中学统计了该校教职工一天行走步数(单位:百步),绘制出如下频率分布直方图:
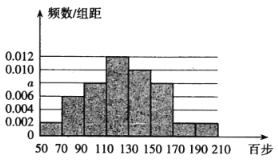
(Ⅰ)求直方图中![]() 的值,并由频率分布直方图估计该校教职工一天步行数的中位数;
的值,并由频率分布直方图估计该校教职工一天步行数的中位数;
(Ⅱ)若该校有教职工175人,试估计一天行走步数不大于130百步的人数;
(Ⅲ)在(Ⅱ)的条件下该校从行走步数大于150百步的3组教职工中用分层抽样的方法选取6人参加远足活动,再从6人中选取2人担任领队,求这两人均来自区间![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() ,
,![]() 是
是![]() 轴上关于原点
轴上关于原点![]() 对称的两定点,点
对称的两定点,点![]() 满足
满足![]() ,点
,点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求![]() 的方程;
的方程;
(2)过![]() 的直线与
的直线与![]() 交于点
交于点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,
,![]() 的中垂线分别与
的中垂线分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,问
,问![]() 是否成立?若成立,求出直线
是否成立?若成立,求出直线![]() 的方程;若不成立,请说明理由.
的方程;若不成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com