Question

一个凸多边形的内角成等差数列，其中最小的内角为120°，公差为5°，那么这个多边形的边数n等于（ ）
A．12
B．16
C．9
D．16或9

Answer 1

【答案】分析：由等差数列的通项公式可得多边形的内角a_n=120°+5°（n-1）=5°n+115°，由n边形内角和定理和等差数列的前n项和公式可得，
（n-2）×180°=n×120°+n（n-1）2×5°．解出即可．
解答：解：由题意可得多边形的内角a_n=120°+5°（n-1）=5°n+115°，
由a_n＜180°，可得n＜13且n∈N^*，
由n边形内角和定理得，
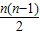
（n-2）×180°=n×120°+×5°．
解得n=16或n=9
∵n＜13，∴n=9．
故选C．
点评：熟练掌握等差数列的通项公式、等差数列的前n项和公式、n边形内角和定理是解题的关键．