
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
| ||||
|
| A、①②④ | B、①②③④ |
| C、①② | D、①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:
又X的数学期望EX=3,则a+b等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源:2010年福建省四地六校高二下学期第二次联考数学(理科)试题 题型:选择题
以下四个命题:
①由圆的过圆心的弦最长的性质类比出球的过球心的的截面面积最大的性质;
②若 ,则
,则 ;
;
③在含有5件次品的100件产品中,任取3件,则取到两件次品的概率为 ;
;
④若离散型随机变量X的方差为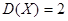 ,则
,则 .
.
其中正确命题的序号是( )
A.①②④ B.①②③④ C.①② D.①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com