
【题目】已知函数![]() ,a∈R.
,a∈R.
(1)求函数f(x)的单调区间;
(2)若f(x)在(1,2)上是单调函数,求a的取值范围.
【答案】(1)见解析;(2)![]() 或
或![]() 或
或![]()
【解析】试题分析:(1)求导,讨论![]() 的取值,研究导数的符号变换得到函数的单调区间;(2)通过研究所给区间和前一问的单调区间的关系进行求解.
的取值,研究导数的符号变换得到函数的单调区间;(2)通过研究所给区间和前一问的单调区间的关系进行求解.
试题解析:(1)f(x)的定义域为{x|x≠a}.f′(x)=![]() .
.
①当a=0时,f′(x)=1,
则f(x)的单调递增区间为(-∞,0),(0,+∞).
②当a>0时,由f′(x)>0,得x>2a或x<0,
此时0<a<2a;由f′(x)<0,得0<x<a或a<x<2a,
则f(x)的单调递增区间为(2a,+∞),(-∞,0),
单调递减区间为(0,a),(a,2a).
③当a<0时,由f′(x)>0,得x>0或x<2a,此时2a<a<0;由f′(x)<0,得2a<x<a或a<x<0,
则函数f(x)的单调递增区间为(-∞,2a),(0,+∞),单调递减区间为(2a,a),(a,0).
(2)①当a≤0时,由(1)可知,f(x)在(1,2)上单调递增,满足题意;
②当0<2a≤1,即0<a≤![]() 时,由(1)可知,f(x)在(2a,+∞)上单调递增,即在(1,2)上单调递增,满足题意;
时,由(1)可知,f(x)在(2a,+∞)上单调递增,即在(1,2)上单调递增,满足题意;
③当1<2a<2,即![]() <a<1时,由(1)可得,f(x)在(1,2)上不具有单调性,不满足题意;
<a<1时,由(1)可得,f(x)在(1,2)上不具有单调性,不满足题意;
④当2a=2,即a=1时,由(1)可知,f(x)在(a,2a)上单调递减,即在(1,2)上单调递减,满足题意;
⑤当1<a<2时,因为f(x)的定义域为{x|x≠a},显然f(x)在(1,2)上不具有单调性,不满足题意;
⑥当a≥2时,由(1)可知,f(x)在(0,a)上单调递减,即在(1,2)上单调递减,满足题意.
综上所述,a≤![]() 或a=1或a≥2.
或a=1或a≥2.


科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为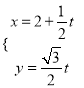 (t为参数),若以该直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ-4cos θ=0.
(t为参数),若以该直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ-4cos θ=0.
(1)求直线l与曲线C的普通方程;
(2)已知直线l与曲线C交于A,B两点,设M(2,0),求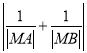 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高三一班、二班各有6名学生去参加学校组织的高中数学竞赛选拔考试,成绩如茎叶图所示.
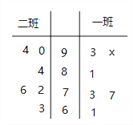
(1)若一班、二班6名学生的平均分相同,求![]() 值;
值;
(2)若将竞赛成绩在![]() 、
、![]() 、
、![]() 内的学生在学校推优时,分别赋分、2分、3分,现在从一班的6名参赛学生中选两名,求推优时,这两名学生赋分的和为4分的概率.
内的学生在学校推优时,分别赋分、2分、3分,现在从一班的6名参赛学生中选两名,求推优时,这两名学生赋分的和为4分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
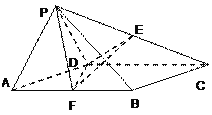
【题目】如图,菱形![]() 与等边
与等边![]() 所在的平面相互垂直,
所在的平面相互垂直, ![]() ,点E,F分别为PC和AB的中点.
,点E,F分别为PC和AB的中点.
(Ⅰ)求证:EF∥平面PAD
(Ⅱ)证明: ![]() ;
;
(Ⅲ)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2-ax+2lnx,a∈R.
(Ⅰ)若曲线y=f(x)在(1,f(1))处的切线垂直于直线y=x,求函数f(x)的单调区间;
(Ⅱ)若x>1时,f(x)>0恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R的函数![]() 是偶函数,且满足
是偶函数,且满足![]() 上的解析式为
上的解析式为![]() ,过点
,过点![]() 作斜率为k的直线l,若直线l与函数
作斜率为k的直线l,若直线l与函数![]() 的图象至少有4个公共点,则实数k的取值范围是
的图象至少有4个公共点,则实数k的取值范围是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856262)
如图所示,在斜三棱柱ABC-A1B1C1中,AB=BC=1,AA1=2,D是AC的中点,AB⊥平面B1C1CB,∠BCC1=60°.
(Ⅰ)求证:AC⊥平面BDC1;
(Ⅱ)E是线段CC1上的动点,判断点E到平面AA1B1B的距离是否为定值,若是,求出此定值;否则,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的离心率为
的离心率为![]() ,右焦点为F,上顶点为A,且△AOF的面积为
,右焦点为F,上顶点为A,且△AOF的面积为![]() (O为坐标原点).
(O为坐标原点).
(1)求椭圆C的方程;
(2)设P是椭圆C上的一点,过P的直线与以椭圆的短轴为直径的圆切于第一象限内的一点M,证明:|PF|+|PM|为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图像在
的图像在![]() 上连续不断,定义:
上连续不断,定义:
![]() (
(![]() ),
),![]() (
(![]() ),其中
),其中![]() 表示函数
表示函数![]() 在
在![]() 上的最小值,
上的最小值, ![]() 表示函数
表示函数![]() 在
在![]() 上的最大值,若存在最小正整数
上的最大值,若存在最小正整数![]() ,使得
,使得![]() 对任意的
对任意的![]() 成立,则称函数
成立,则称函数![]() 为
为![]() 上的“
上的“![]() 阶收缩函数”.
阶收缩函数”.
(1)若![]() ,
, ![]() ,试写出
,试写出![]() ,
, ![]() 的表达式;
的表达式;
(2)已知函数![]() ,
, ![]() ,判断
,判断![]() 是否为
是否为![]() 上的“
上的“![]() 阶收缩函数”,如果是,求出对应的
阶收缩函数”,如果是,求出对应的![]() ,如果不是,请说明理由;
,如果不是,请说明理由;
(3)已知![]() ,函数
,函数![]() ,是
,是![]() 上的2阶收缩函数,求
上的2阶收缩函数,求![]() 的取值范围.
的取值范围.
数学附加题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com