
【题目】已知椭圆C: ![]() =1(a>b>0)的左焦点为F,直线y=kx(k>0)与椭圆C交于A,B两点,若
=1(a>b>0)的左焦点为F,直线y=kx(k>0)与椭圆C交于A,B两点,若 ![]() ,则C的离心率取值范围为( )
,则C的离心率取值范围为( )
A.![]()
B.![]()
C.![]()
D.![]()
 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】设F1 , F2是椭圆 ![]() (0<b<2)的左、右焦点,过F1的直线l交椭圆于A,B两点,若|AF2|+|BF2|最大值为5,则椭圆的离心率为( )
(0<b<2)的左、右焦点,过F1的直线l交椭圆于A,B两点,若|AF2|+|BF2|最大值为5,则椭圆的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】极坐标系中椭圆C的方程为ρ2= ![]() ,以极点为原点,极轴为x轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.
,以极点为原点,极轴为x轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.
(1)若椭圆上任一点坐标为P(x,y),求 ![]() 的取值范围;
的取值范围;
(2)若椭圆的两条弦AB,CD交于点Q,且直线AB与CD的倾斜角互补,求证:|QA||QB|=|QC||QD|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,平面BFED⊥平面ABCD,BF=1.
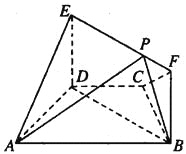
(1)求证:AD⊥平面BFED;
(2)已知点P在线段EF上,![]() =2.求三棱锥E-APD的体积.
=2.求三棱锥E-APD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
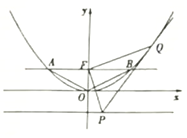
【题目】已知抛物线![]() 的焦点为F,过F作平行于x轴的直线交抛物线于A,B两点(A在B的左侧),若△AOB的面积为2.
的焦点为F,过F作平行于x轴的直线交抛物线于A,B两点(A在B的左侧),若△AOB的面积为2.
(1)求抛物线C的方程;
(2)设P是抛物线C的准线上一点,Q是抛物线上的一点,若PF⊥QF,求证:直线PQ与抛物线相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
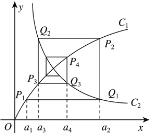
【题目】如图所示,已知曲线C1:y=![]() (x>0)及曲线C2:y=
(x>0)及曲线C2:y=![]() (x>0).C1上的点Pn的横坐标为an,
(x>0).C1上的点Pn的横坐标为an,![]() 过C1上的点Pn(n∈N+)作直线平行于x轴,交曲线C2于点Qn,再过点Qn作直线平行于y轴,交曲线C1于点Pn+1.
过C1上的点Pn(n∈N+)作直线平行于x轴,交曲线C2于点Qn,再过点Qn作直线平行于y轴,交曲线C1于点Pn+1.
试求an+1与an之间的关系,并证明a2n-1<![]() <a2n(n∈N+).
<a2n(n∈N+).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2013年,首都北京经历了59年来雾霾天气最多的一个月.经气象局统计,北京市从1月1日至1月30日的30天里有26天出现雾霾天气,《环境空气质量指数(AQI)技术规定(试行)》将空气质量指数分为六级,其中,中度污染(四级)指数为151~200;重度污染(五级)指数为201~300;严重污染(六级)指数大于300.下面表1是某观测点记录的4天里AQI指数M与当天的空气水平可见度y(千米)的情况,表2是某气象观测点记录的北京1月1日到1月30日AQI指数频数的统计结果.
表1
AQI指数M | 900 | 700 | 300 | 100 |
空气可见度y/千米 | 0.5 | 3.5 | 6.5 | 9.5 |
表2
AQI指数 | [0,200] | (200,400] | (400,600] | (600,800] | (800,1000] |
频数 | 3 | 6 | 12 | 6 | 3 |
(1)设变量x=![]() ,根据表1的数据,求出y关于x的线性回归方程;
,根据表1的数据,求出y关于x的线性回归方程;
(2)根据表2估计这30天AQI指数的平均值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com