
| π |
| 4 |
| π |
| 4 |
| OP |
| OQ |
| OP |
| OQ |
| ||||
|
|
| ||||
|
|
| OP |
| OQ |
| OP |
| OQ |
| OP |
| OQ |
| ||||
|
|
| 2cosx |
| 1+cos2x |
| ||||
|
|
| 2cosx |
| 1+cos2x |
| 2 | ||
cosx+
|
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
| 1 |
| x |
| ||
| 2 |
| 1 |
| x2 |
| ||
| 2 |
| 1 |
| x |
| ||
| 2 |
| 1 |
| cosx |
3
| ||
| 2 |
2
| ||
| 3 |
2
| ||
| 3 |


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源:黄冈重点作业·高三数学(下) 题型:044
平面直角坐标系有点P(1,cosx),Q(cosx,1),(x∈[- ,
, ]).
]).
(1)求向量 和
和 的夹角θ的余弦用x表示的函数f(x);
的夹角θ的余弦用x表示的函数f(x);
(2)求θ的最值.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| π |
| 4 |
| π |
| 4 |
| OP |
| OQ |
查看答案和解析>>
科目:高中数学 来源:《第3章 三角恒等变换》2013年单元测试卷1(解析版) 题型:解答题
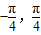 ];
];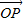 和
和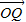 的夹角θ的余弦用x表示的函数f(x);
的夹角θ的余弦用x表示的函数f(x);查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省聊城市某重点中学高二(上)期末数学试卷(理科)(解析版) 题型:解答题
 ];
]; 和
和 的夹角θ的余弦用x表示的函数f(x);
的夹角θ的余弦用x表示的函数f(x);查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com