
【题目】下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.
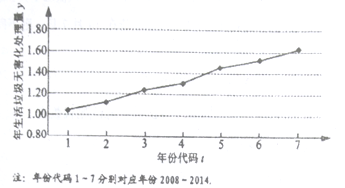
(1)由折线图看出,可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)建立![]() 关于
关于![]() 的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
参考数据: ![]() ,
, ![]() ,
, 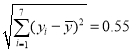 ,
, ![]() .
.
参考公式:相关系数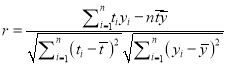
回归方程![]() 中,
中, 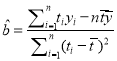 ,
, ![]() .
.
【答案】(1)可以用线性回归模型拟合![]() 与
与![]() 的关系;(2)1.82亿吨.
的关系;(2)1.82亿吨.
【解析】试题分析:(1)由折线图看出, ![]() 与
与![]() 之间存在较强的正相关关系,将已知数据代入相关系数方程,可得答案;(2)根据已知中的数据,求出回归系数,可得回归方程,2016年应的
之间存在较强的正相关关系,将已知数据代入相关系数方程,可得答案;(2)根据已知中的数据,求出回归系数,可得回归方程,2016年应的![]() 值为
值为![]() ,代入可预测2016年我国生活垃圾无害化处理量.
,代入可预测2016年我国生活垃圾无害化处理量.
试题解析:(1)由折线图数据和参考数据得: ![]() ,
, ![]() ,
,
所以,相关系数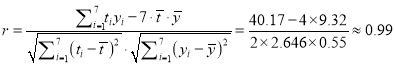
因为![]() 与
与![]() 的相关系数近似为0.99,说明
的相关系数近似为0.99,说明![]() 与
与![]() 的线性相关程度相当高,从而可以用线性回归模型拟合
的线性相关程度相当高,从而可以用线性回归模型拟合![]() 与
与![]() 的关系。
的关系。
(2)由![]() 及(1)得
及(1)得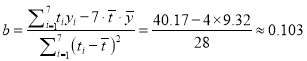 ,
, ![]() ,所以
,所以![]() 与
与![]() 的回归方程为
的回归方程为![]()
将2016年对应的![]() 代入回归方程得:
代入回归方程得: ![]() ,所以预测2016年我国生活垃圾无害化处理量将约1.82亿吨.
,所以预测2016年我国生活垃圾无害化处理量将约1.82亿吨.
【方法点晴】本题主要考查折线图和线性回归方程的应用,属于中档题.求回归直线方程的步骤:①依据样本数据画出散点图,确定两个变量具有线性相关关系;②计算![]() 的值;③计算回归系数
的值;③计算回归系数![]() ;④写出回归直线方程为
;④写出回归直线方程为![]() ;(2) 回归直线过样本点中心
;(2) 回归直线过样本点中心![]() 是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.
是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.


科目:高中数学 来源: 题型:
【题目】一次猜奖游戏中,1,2,3,4四扇门里摆放了![]() ,
, ![]() ,
, ![]() ,
, ![]() 四件奖品(每扇门里仅放一件).甲同学说:1号门里是
四件奖品(每扇门里仅放一件).甲同学说:1号门里是![]() ,3号门里是
,3号门里是![]() ;乙同学说:2号门里是
;乙同学说:2号门里是![]() ,3号门里是
,3号门里是![]() ;丙同学说:4号门里是
;丙同学说:4号门里是![]() ,2号门里是
,2号门里是![]() ;丁同学说:4号门里是
;丁同学说:4号门里是![]() ,3号门里是
,3号门里是![]() .如果他们每人都猜对了一半,那么4号门里是( )
.如果他们每人都猜对了一半,那么4号门里是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为自然对数的底数,
为自然对数的底数,![]() ),
),![]() (
(![]() ,
,![]()
![]() ),
),
⑴若![]() ,
,![]() .求
.求![]() 在
在![]() 上的最大值
上的最大值![]() 的表达式;
的表达式;
⑵若![]() 时,方程
时,方程![]() 在
在![]() 上恰有两个相异实根,求实根
上恰有两个相异实根,求实根![]() 的取值范围;
的取值范围;
⑶若![]() ,
,![]() ,求使
,求使![]() 得图像恒在
得图像恒在![]() 图像上方的最大正整数
图像上方的最大正整数![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过研究学生的学习行为,心理学家发现,学生接受能力依赖于老师引入概念和描述问题所用的时间,讲座开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持理想的状态,随后学生的注意力开始分散,分析结果和实验表明,用![]() 表示学生掌握和接受概念的能力(
表示学生掌握和接受概念的能力(![]() 的值越大,表示接受能力越强),
的值越大,表示接受能力越强),![]() 表示提出和讲授概念的时间(单位:分),可以有以下公式:
表示提出和讲授概念的时间(单位:分),可以有以下公式: 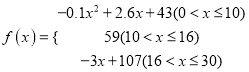 .
.
(1)开讲多少分钟后,学生的接受能力最强?能维持多少分钟?
(2)开讲5分钟与开讲20分钟比较,学生的接受能力何时强一些?
(3)一个数学难题,需要55的接受能力以及13分钟的时间,老师能否及时在学生一直达到所需接受能力的状态下讲授完这个难题?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C对边的边长分别是a,b,c.已知c=2,C=![]() .
.
(1)若△ABC的面积等于![]() ,求a,b;
,求a,b;
(2)若sinC+sin(B-A)=2sin2A,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:①集合![]() 的子集个数有16个;②定义在
的子集个数有16个;②定义在![]() 上的奇函数
上的奇函数![]() 必满足
必满足![]() ;③
;③![]() 既不是奇函数又不是偶函数;④偶函数的图像一定与
既不是奇函数又不是偶函数;④偶函数的图像一定与![]() 轴相交;⑤
轴相交;⑤![]() 在
在![]() 上是减函数。
上是减函数。
其中真命题的序号是 ______________(把你认为正确的命题的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前3项和为6,前8项和为-4.
(1)求数列{an}的通项公式;
(2)设bn=(4-an)qn-1 (q≠0,n∈N*),求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】东莞市某高级中学在今年4月份安装了一批空调,关于这批空调的使用年限![]() (单位:年,
(单位:年, ![]() )和所支出的维护费用
)和所支出的维护费用![]() (单位:万元)厂家提供的统计资料如下:
(单位:万元)厂家提供的统计资料如下:

(1)请根据以上数据,用最小二乘法原理求出维护费用![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若规定当维护费用![]() 超过13.1万元时,该批空调必须报废,试根据(1)的结论求该批空调使用年限的最大值.
超过13.1万元时,该批空调必须报废,试根据(1)的结论求该批空调使用年限的最大值.
参考公式:最小二乘估计线性回归方程![]() 中系数计算公式:
中系数计算公式:
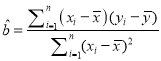 ,
, ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com