
【题目】某科研课题组通过一款手机APP软件,调查了某市1000名跑步爱好者平均每周的跑步量(简称“周跑量”),得到如下的频数分布表
周跑量(km/周) |
|
|
|
|
|
|
|
|
|
人数 | 100 | 120 | 130 | 180 | 220 | 150 | 60 | 30 | 10 |
(1)在答题卡上补全该市1000名跑步爱好者周跑量的频率分布直方图:

注:请先用铅笔画,确定后再用黑色水笔描黑
(2)根据以上图表数据计算得样本的平均数为![]() ,试求样本的中位数(保留一位小数),并用平均数、中位数等数字特征估计该市跑步爱好者周跑量的分布特点
,试求样本的中位数(保留一位小数),并用平均数、中位数等数字特征估计该市跑步爱好者周跑量的分布特点
(3)根据跑步爱好者的周跑量,将跑步爱好者分成以下三类,不同类别的跑者购买的装备的价格不一样,如下表:
周跑量 | 小于20公里 | 20公里到40公里 | 不小于40公里 |
类别 | 休闲跑者 | 核心跑者 | 精英跑者 |
装备价格(单位:元) | 2500 | 4000 | 4500 |
根据以上数据,估计该市每位跑步爱好者购买装备,平均需要花费多少元?
【答案】(1)见解析;(2) 中位数为29.2,分布特点见解析; (3)3720元
【解析】
(1)根据频数和频率之间的关系计算,即可得到答案;
(2)根据频率分布直方图利用中位数两边频率相等,列方程求出中位数的值,进而得出结论;
(3)根据频率分布直方图求出休闲跑者,核心跑者,精英跑者分别人数,进而求出平均值.
(1)补全该市1000名跑步爱好者周跑量的频率分布直方图,如下:
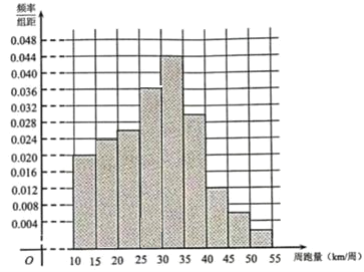
(2)中位数的估计值:
由![]() ,
,![]()
所以中位数位于区间![]() 中,
中,
设中位数为![]() ,则
,则![]() ,
,
解得![]() ,因为
,因为![]() ,
,
所以估计该市跑步爱好者多数人的周跑量多于样本的平均数.
(3)依题意可知,休闲跑者共有![]() 人,
人,
核心跑者![]() 人,
人,
精英跑者![]() 人,
人,
所以该市每位跑步爱好者购买装备,平均需要![]() 元.
元.


科目:高中数学 来源: 题型:
【题目】李克强总理在2018年政府工作报告指出,要加快建设创新型国家,把握世界新一轮科技革命和产业变革大势,深入实施创新驱动发展战略,不断增强经济创新力和竞争力.某手机生产企业积极响应政府号召,大力研发新产品,争创世界名牌.为了对研发的一批最新款手机进行合理定价,将该款手机按事先拟定的价格进行试销,得到一组销售数据![]() ,如表所示:
,如表所示:
单价 |
|
|
|
|
|
|
销量 |
|
|
|
|
|
|
已知![]() .
.
(1)若变量![]() 具有线性相关关系,求产品销量
具有线性相关关系,求产品销量![]() (百件)关于试销单价
(百件)关于试销单价![]() (千元)的线性回归方程
(千元)的线性回归方程![]() ;
;
(2)用(1)中所求的线性回归方程得到与![]() 对应的产品销量的估计值
对应的产品销量的估计值![]() .
.
(参考公式:线性回归方程中![]() 的估计值分别为
的估计值分别为 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方体ABCD﹣A1B1C1D1的棱长为1,点E,F分别是棱D1C1 , B1C1的中点,过E,F作一平面α,使得平面α∥平面AB1D1 , 则平面α截正方体的表面所得平面图形为( )
A.三角形
B.四边形
C.五边形
D.六边形
查看答案和解析>>
科目:高中数学 来源: 题型:
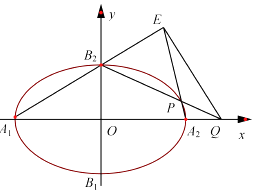
【题目】如图,椭圆 ![]() 的离心率为
的离心率为 ![]() ,顶点为A1、A2、B1、B2 , 且
,顶点为A1、A2、B1、B2 , 且 ![]() .
.
(1)求椭圆C的方程;
(2)P是椭圆C上除顶点外的任意点,直线B2P交x轴于点Q,直线A1B2交A2P于点E.设A2P的斜率为k,EQ的斜率为m,试问2m﹣k是否为定值?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市教育部门为了解全市高三学生的身高发育情况,从本市全体高三学生中随机抽取了100人的身高数据进行统计分析.经数据处理后,得到了如下图1所示的频事分布直方图,并发现这100名学生中,身高不低于1.69米的学生只有16名,其身高茎叶图如下图2所示,用样本的身高频率估计该市高一学生的身高概率.
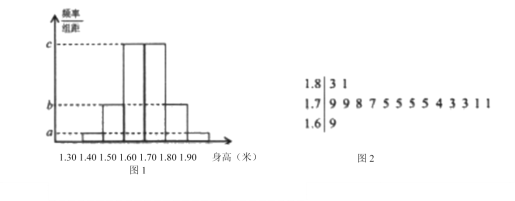
(1)求该市高三学生身高高于1.70米的概率,并求图1中![]() 、
、![]() 、
、![]() 的值.
的值.
(2)若从该市高三学生中随机选取3名学生,记![]() 为身高在
为身高在![]() 的学生人数,求
的学生人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)若变量![]() 满足
满足![]() 且
且![]() ,则称变量
,则称变量![]() 满足近似于正态分布
满足近似于正态分布![]() 的概率分布.如果该市高三学生的身高满足近似于正态分布
的概率分布.如果该市高三学生的身高满足近似于正态分布![]() 的概率分布,则认为该市高三学生的身高发育总体是正常的.试判断该市高三学生的身高发育总体是否正常,并说明理由.
的概率分布,则认为该市高三学生的身高发育总体是正常的.试判断该市高三学生的身高发育总体是否正常,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某射手射击1次,击中目标的概率是0.9,他连续射击4次,且他各次射击是否击中目标相互之间没有影响.有下列结论:
①他第3次击中目标的概率是0.9; ②他恰好击中目标3次的概率是0.93×0.1;
③他至少击中目标1次的概率是1-0.14 ④他恰好有连续2次击中目标的概率为3×0.93×0.1
其中正确结论的序号是______
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在2012年的自主招生考试成绩中随机抽取![]() 名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 |
|
第2组 |
| ① |
|
第3组 |
| 30 | ② |
第4组 |
| 20 |
|
第5组 |
| 10 |
|

(1)请先求出频率分布表中![]() 位置的相应数据,再完成频率分布直方图;
位置的相应数据,再完成频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第![]() 组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
(3)在(2)的前提下,学校决定在![]() 名学生中随机抽取
名学生中随机抽取![]() 名学生接受
名学生接受![]() 考官进行面试,求:第
考官进行面试,求:第![]() 组至少有一名学生被考官
组至少有一名学生被考官![]() 面试的概率.
面试的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com