
【题目】已知椭圆![]() 的离心率
的离心率![]() ,且椭圆过点
,且椭圆过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 在
在![]() 上,
上,![]() 是坐标原点,若
是坐标原点,若![]() ,判断四边形
,判断四边形![]() 的面积是否为定值?若为定值,求出该定值;如果不是,请说明理由.
的面积是否为定值?若为定值,求出该定值;如果不是,请说明理由.
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:
【题目】某大城市一家餐饮企业为了了解外卖情况,统计了某个送外卖小哥某天从9:00到21:00这个时间段送的50单外卖.以2小时为一时间段将时间分成六段,各时间段内外卖小哥平均每单的收入情况如下表,各时间段内送外卖的单数的频率分布直方图如下图.
时间区间 |
|
|
|
|
|
|
每单收入(元) | 6 | 5.5 | 6 | 6.4 | 5.5 | 6.5 |
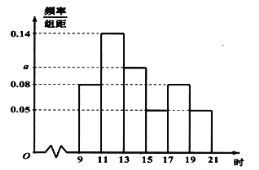
(Ⅰ)求频率分布直方图中![]() 的值,并求这个外卖小哥送这50单获得的收入;
的值,并求这个外卖小哥送这50单获得的收入;
(Ⅱ)在这个外卖小哥送出的50单外卖中男性订了25单,且男性订的外卖中有20单带饮品,女性订的外卖中有10单带饮品,请完成下面的![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为“带饮品和男女性别有关”?
的把握认为“带饮品和男女性别有关”?
带饮品 | 不带饮品 | 总计 | |
男 | |||
女 | |||
总计 |
附:![]()
| 0.050 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记无穷数列![]() 的前
的前![]() 项中最大值为
项中最大值为![]() ,最小值为
,最小值为![]() ,令
,令![]() .
.
(1)若![]() ,写出
,写出![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)设![]() ,若
,若![]() ,求
,求![]() 的值及
的值及![]() 时数列
时数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)求证:“数列![]() 是等差数列”的充要条件是“数列
是等差数列”的充要条件是“数列![]() 是等差数列”.
是等差数列”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C:![]() (a>0,b>0)的渐近线方程为y=±
(a>0,b>0)的渐近线方程为y=±![]() x,右顶点为(1,0).
x,右顶点为(1,0).
(1)求双曲线C的方程;
(2)已知直线y=x+m与双曲线C交于不同的两点A,B,且线段AB的中点为![]() ,当x0≠0时,求
,当x0≠0时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=2,AB//DC,AB=2CD,∠BCD=90°.
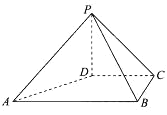
(1)求证:AD⊥PB;
(2)求点C到平面PAB的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】七巧板是古代中国劳动人民发明的一种中国传统智力玩具,它由五块等腰直角三角形,一块正方形和一块平行四边形共七块板组成.清陆以湉《冷庐杂识》卷一中写道:近又有七巧图,其式五,其数七,其变化之式多至千余.体物肖形,随手变幻,盖游戏之具,足以排闷破寂,故世俗皆喜为之.如图是一个用七巧板拼成的正方形,若在此正方形中任取一点,则此点取自阴影部分的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ;直线
;直线![]() 的参数方程为
的参数方程为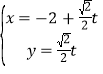 (t为参数).直线
(t为参数).直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上,且
上,且![]() ,
,![]() ,现将
,现将![]() 沿
沿![]() 折到
折到![]() 的位置,连结
的位置,连结![]() ,
,![]() ,如图2
,如图2
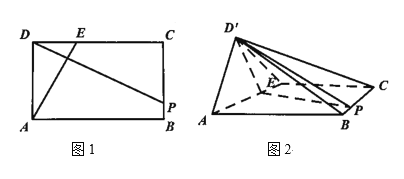
(1)证明:![]() ;
;
(2)记平面![]() 与平面
与平面![]() 的交线为
的交线为![]() .若二面角
.若二面角![]() 为
为![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com