
【题目】已知 ![]() =(2cosx,sinx﹣cosx),
=(2cosx,sinx﹣cosx), ![]() =(
=( ![]() sinx,sinx+cosx),记函数f(x)=
sinx,sinx+cosx),记函数f(x)= ![]()
![]() . (Ⅰ)求f(x)的表达式,以及f(x)取最大值时x的取值集合;
. (Ⅰ)求f(x)的表达式,以及f(x)取最大值时x的取值集合;
(Ⅱ)设△ABC三内角A,B,C的对应边分别为a,b,c,若a+b=2 ![]() ,c=
,c= ![]() ,f(C)=2,求△ABC的面积.
,f(C)=2,求△ABC的面积.
【答案】解:(Ⅰ)f(x)= ![]()
![]() =2
=2 ![]() sinxcosx+sin2x﹣cos2x=
sinxcosx+sin2x﹣cos2x= ![]() sin2x﹣cos2x=2sin(2x﹣
sin2x﹣cos2x=2sin(2x﹣ ![]() ), 当2x﹣
), 当2x﹣ ![]() =2kπ+
=2kπ+ ![]() (k∈Z)时,f(x)max=2,
(k∈Z)时,f(x)max=2,
对应x的集合为{x|x=kπ+ ![]() ,k∈Z}.
,k∈Z}.
(Ⅱ)由f(C)=2,得2sin(2C﹣ ![]() )=1,
)=1,
∵0<C<π,∴﹣ ![]() <2C﹣
<2C﹣ ![]() <
< ![]() ,∴2C﹣
,∴2C﹣ ![]() =
= ![]() ,解得C=
,解得C= ![]() ,
,
又∵a+b=2 ![]() ,c=
,c= ![]() ,由余弦定理得c2=a2+b2﹣ab,
,由余弦定理得c2=a2+b2﹣ab,
∴12﹣3ab=6,即ab=2,…
由面积公式得△ABC面积为S△ABC= ![]() =
= ![]() .
.
【解析】(Ⅰ)f(x)= ![]()
![]() =2
=2 ![]() sinxcosx+sin2x﹣cos2x=
sinxcosx+sin2x﹣cos2x= ![]() sin2x﹣cos2x=2sin(2x﹣
sin2x﹣cos2x=2sin(2x﹣ ![]() ),利用三角函数的性质,即可求出f(x)取最大值时x的取值集合;(Ⅱ)先求出C,再求出△ABC的面积.
),利用三角函数的性质,即可求出f(x)取最大值时x的取值集合;(Ⅱ)先求出C,再求出△ABC的面积.
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识,掌握正弦定理:![]() ,以及对余弦定理的定义的理解,了解余弦定理:
,以及对余弦定理的定义的理解,了解余弦定理:![]() ;
;![]() ;
;![]() .
.


科目:高中数学 来源: 题型:
【题目】某省每年损失耕地20万亩,每亩耕地价值24000元,为了减少耕地损失,决定按耕地价格的t%征收耕地占用税,这样每年的耕地损失可减少 ![]() t万亩,为了既可减少耕地的损失又保证此项税收一年不少于9000万元,则t的取值范围是( )
t万亩,为了既可减少耕地的损失又保证此项税收一年不少于9000万元,则t的取值范围是( )
A.[1,3]
B.[3,5]
C.[5,7]
D.[7,9]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,右焦点为F,椭圆与y轴的正半轴交于点B,且|BF|=
,右焦点为F,椭圆与y轴的正半轴交于点B,且|BF|= ![]() .
.
(1)求椭圆E的方程;
(2)若斜率为1的直线l经过点(1,0),与椭圆E相交于不同的两点M,N,在椭圆E上是否存在点P,使得△PMN的面积为 ![]() ,请说明理由.
,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x∈[1,2],x2﹣a≥0;命题q:x0∈R,使得 ![]() +(a﹣1)x0+1<0.若“p或q”为真,“p且q”为假,则实数a的取值范围
+(a﹣1)x0+1<0.若“p或q”为真,“p且q”为假,则实数a的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an},{bn}中,已知a1=2,b1=4,且﹣an , bn , an+1成等差数列,﹣bn , an , bn+1也成等差数列. (Ⅰ)求证:数列{an+bn}和{an﹣bn}都是等比数列,并求数列{an}的通项公式;
(Ⅱ)若cn=(an﹣3n)log3[an﹣(﹣1)n],求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数y=f(x)的图象上每一点的纵坐标保持不变,横坐标伸长到原来的2倍,再将整个图象沿x轴向右平移 ![]() 个单位,沿y轴向下平移1个单位,得到函数y=
个单位,沿y轴向下平移1个单位,得到函数y= ![]() sinx的图象,则y=f(x)的解析式为( )
sinx的图象,则y=f(x)的解析式为( )
A.y= ![]() sin(2x+
sin(2x+ ![]() )+1
)+1
B.y= ![]() sin(2x﹣
sin(2x﹣ ![]() )+1
)+1
C.y= ![]() sin(
sin( ![]() x+
x+ ![]() )+1
)+1
D.y= ![]() sin(
sin( ![]() x﹣
x﹣ ![]() )+1
)+1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(其中 ![]() )的图象如图所示,为了得到g(x)=sin2x的图象,则只需将f(x)的图象( )
)的图象如图所示,为了得到g(x)=sin2x的图象,则只需将f(x)的图象( ) 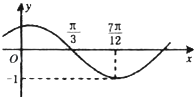
A.向右平移 ![]() 个长度单位
个长度单位
B.向右平移 ![]() 个长度单位
个长度单位
C.向左平移 ![]() 个长度单位
个长度单位
D.向左平移 ![]() 个长度单位
个长度单位
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com