练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆上的焦点为，离心率为．

    （1）求椭圆方程；

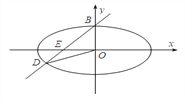
    （2）设过椭圆顶点，斜率为的直线交椭圆于另一点，交轴于点，且， ， 成等比数列，求的值．

    【答案】(1) 椭圆的方程为;(2)当， ， 成等比数列时， .

    【解析】试题分析：（Ⅰ）由椭圆的性质容易求出参数a,b的值，从而求出椭圆方程；（Ⅱ）设出直线方程，代入椭圆方程，求出点D、E的坐标，然后利用|BD|，|BE|，|DE|成等比数列，即可求解．

    试题解析：（Ⅰ）由已知．解得，所以，椭圆的方程为．

    （Ⅱ）由（Ⅰ）得过B点的直线为，由得，所以，所以，依题意．因为|BD|，|BE|，|DE|成等比数列，所以，所以，即，当时， ，无解，当时， ，解得，所以，当|BD|，|BE|，|DE|成等比数列时， ．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （1）讨论的单调性；

    （2）当有最大值，且最大值大于时，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

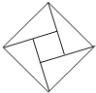
    【题目】在北京召开的第24届国际数学家大会会标如图所示，它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形．若直角三角形中较小的锐角记作，大正方形的面积是1，小正方形的面积是，则的值等于（ ）

    A. 1 B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （1）判断函数的单调性，并说明理由

    （2）若对任意的恒成立，求a的取值范围

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数是定义在上的偶函数，且对任意的恒有，已知当时，，则下列命题：

    ①对任意，都有；②函数在上递减，在上递增；

    ③函数的最大值是1，最小值是0；④当时，.

    其中正确命题的序号有________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】不等式|x﹣ ≤ 的解集为{x|n≤x≤m}
    （1）求实数m，n；
    （2）若实数a，b满足：|a+b|＜m，|2a﹣b|＜n，求证：|b|＜ ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设定义在（0，+∞）的单调函数f（x），对任意的x∈（0，+∞）都有f[f（x）﹣log2x]=6．若x0是方程f（x）﹣f′（x）=4的一个解，且 ，则a=（ ）
    A.4
    B.3
    C.2
    D.1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（其中），若的一条对称轴离最近的对称中心的距离为．

    （Ⅰ）求的单调递增区间；

    （Ⅱ）在中角、、的对边分别是满足恰是的最大值，试判断的形状．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知 ， ： ， ： ．

    （1）若 是 的充分条件，求实数 的取值范围；

    （2）若 ，“”为真命题，“”为假命题，求实数 的取值范围．

    查看答案和解析>>

    同步练习册答案