
分析 由立方差公式得到$(\root{3}{2}-1)$•a=2-1=1,再化简,构造立方差公式计算即可.
解答 解:∵$(\root{3}{2}-1)$•a=2-1=1,
∴$\frac{1}{a}$=$\root{3}{2}$-1,
∴$\frac{3}{a}$+$\frac{3}{{a}^{2}}$+$\frac{1}{{a}^{3}}$=$\frac{3{a}^{2}+3a+1}{{a}^{3}}$=$\frac{{a}^{3}+3{a}^{2}+3a+1}{{a}^{3}}$-1=($\frac{a+1}{a}$)3-1=(1+$\frac{1}{a}$)3-1=1,
故答案为:1.
点评 本题考查了立方差公式,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 4 | C. | 10 | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜爱程度 | 非常喜欢 | 一般 | 不喜欢 |
| 人数 | 500 | 200 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
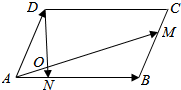 如图所示,□ABCD中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,BM=$\frac{2}{3}$BC,AN=$\frac{1}{4}$AB,
如图所示,□ABCD中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,BM=$\frac{2}{3}$BC,AN=$\frac{1}{4}$AB,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 至少有一个红球与都是黑球 | B. | 至少有一个红球与恰有一个黑球 | ||
| C. | 至少有一个红球与至少有一个黑球 | D. | 恰有一个红球与恰有两个红球 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com