考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:计算题,函数的性质及应用,导数的综合应用
分析:(I)求导f′(x)=-
,从而由导数的正负确定函数的单调区间;
(II)由f(x)的单调增区间为(0,1),单调减区间为(1,+∞)得t<1<t+
,从而解得;
(III)不等式f(x)≥
可化为a≤
,令g(x)=
,从而化恒成立为a≤g
min(x),(x≥1);从而转化为函数的最值问题.
解答:
解:(I)∵f(x)=
,x>0,故f′(x)=-
,
则当x∈(0,1)时,f′(x)>0,当x∈(1,+∞)时,f′(x)<0;
故f(x)的单调增区间为(0,1),单调减区间为(1,+∞);
(II)∵f(x)的单调增区间为(0,1),单调减区间为(1,+∞);
∴t<1<t+
,
故
<t<1;
故实数t的取值范围为(
,1);
(III)不等式f(x)≥
可化为a≤
,
令g(x)=
,
则当x≥1时,不等式f(x)≥
恒成立可化为
a≤g
min(x),(x≥1);
而g′(x)=
;
令h(x)=x-lnx;则h′(x)=1-
≥0;
故h(x)在[1,+∞)上是增函数,
故h(x)≥h(1)≥1;
故g′(x)=
>0;
故g(x)=
在[1,+∞)上是增函数,
故g
min(x)=g(1)=2,
故a≤2;
故实数a的取值范围为(-∞,2].
点评:本题了函数的综合应用及导数的综合应用,同时考查了恒成立问题,属于中档题.



 备战中考寒假系列答案
备战中考寒假系列答案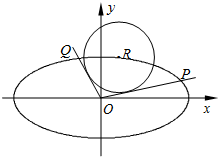 如图,在平面直角坐标系xOy中,已知椭圆C:
如图,在平面直角坐标系xOy中,已知椭圆C: