
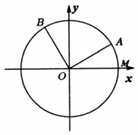
 如图,已知单位圆O与x轴正半轴相交于点M,点A,B在单位圆上,其中点A在第一象限,且∠AOB=$\frac{π}{2}$,记∠MOA=α,∠MOB=β.
如图,已知单位圆O与x轴正半轴相交于点M,点A,B在单位圆上,其中点A在第一象限,且∠AOB=$\frac{π}{2}$,记∠MOA=α,∠MOB=β.分析 (Ⅰ)若α=$\frac{π}{6}$,直接利用三角函数的定义求点A,B的坐标;
(Ⅱ)若点A的坐标为($\frac{4}{5}$,m),则sinα=$\frac{3}{5}$,cosα=sinβ=$\frac{4}{5}$,即可求sinα-sinβ的值.
解答 解:(Ⅰ)若α=$\frac{π}{6}$,则点A($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),B(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$);
(Ⅱ)若点A的坐标为($\frac{4}{5}$,$\frac{3}{5}$),则sinα=$\frac{3}{5}$,cosα=sinβ=$\frac{4}{5}$,
∴sinα-sinβ=-$\frac{1}{5}$.
点评 本题考查任意角的三角函数的定义、诱导公式的应用,比较基础.


科目:高中数学 来源: 题型:选择题
| A. | 偶函数 | B. | 奇函数 | ||
| C. | 定义域上的增函数 | D. | 定义域上的减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 离心率相等 | B. | 虚半轴长相等 | C. | 实半轴长相等 | D. | 焦距相等 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
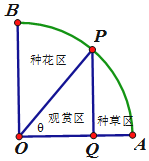 如图,一个圆心角为直角的扇形AOB 花草房,半径为1,点P 是花草房弧上一个动点,不含端点,现打算在扇形BOP 内种花,PQ⊥OA,垂足为Q,PQ 将扇形AOP
如图,一个圆心角为直角的扇形AOB 花草房,半径为1,点P 是花草房弧上一个动点,不含端点,现打算在扇形BOP 内种花,PQ⊥OA,垂足为Q,PQ 将扇形AOP 查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直线 | B. | 椭圆 | C. | 双曲线 | D. | 圆 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≥9 | B. | a≤9 | C. | a≤8 | D. | a≥8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com