
【题目】已知![]() ,
, ![]() 满足约束条件
满足约束条件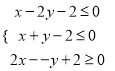 ,若
,若![]() 取得最大值的最优解不唯一,则实数
取得最大值的最优解不唯一,则实数![]() 的值为__________.
的值为__________.
【答案】![]() 或
或![]()
【解析】由题可知若![]() 取得最大值的最优解不唯一则
取得最大值的最优解不唯一则![]() 必平行于可行域的某一边界,如图:
必平行于可行域的某一边界,如图: 要Z最大则直线与y轴的截距最大即可,当a<0时,则平行AC直线即可故a=-2,当a>0时,则直线平行AB即可,故a=1
要Z最大则直线与y轴的截距最大即可,当a<0时,则平行AC直线即可故a=-2,当a>0时,则直线平行AB即可,故a=1
点睛:线性规划为常考题型,解决此题务必要理解最优解个数为无数个时的条件是什么,然后根据几何关系求解即可
【题型】填空题
【结束】
16
【题目】《数书九章》三斜求积术:“以小斜幂,并大斜幂,减中斜幂,余半之,自乘于上;以小斜幂乘大斜幂,减上,余四约一,为实,一为从隅,开平方得积”.秦九韶把三角形的三条边分别称为小斜、中斜和大斜,“术”即方法.以![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别表示三角形的面积,大斜,中斜,小斜;
分别表示三角形的面积,大斜,中斜,小斜; ![]() ,
, ![]() ,
, ![]() 分别为对应的大斜,中斜,小斜上的高;则
分别为对应的大斜,中斜,小斜上的高;则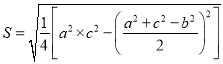
![]()
![]() .若在
.若在![]() 中
中![]() ,
, ![]() ,
, ![]() ,根据上述公式,可以推出该三角形外接圆的半径为__________.
,根据上述公式,可以推出该三角形外接圆的半径为__________.
科目:高中数学 来源: 题型:
【题目】某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,记其质量指标值为M,当M≥85时,产品为一级品;当75≤M<85时,产品为二级品;当70≤M<75时,产品为三级品.现用两种新配方(分别称为A配方和B配方)做实验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
A配方的频数分布表

B配方的频数分布表

(1)从A配方生产的产品中按等级分层抽样抽取5件产品,再从这5件产品中任取3件,求恰好取到1件二级品的频率;
(2)若这种新产品的利润率y与质量指标M满足如下条件: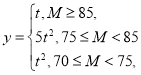 其中t∈
其中t∈![]() ,请分别计算两种配方生产的产品的平均利润率,如果从长期来看,你认为投资哪种配方的产品平均利润率较大?
,请分别计算两种配方生产的产品的平均利润率,如果从长期来看,你认为投资哪种配方的产品平均利润率较大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,AB//CD,∠ABC=![]() ,BC=CD=CE=1,EC⊥平面ABCD,EF
,BC=CD=CE=1,EC⊥平面ABCD,EF![]() AC,P是线段EF上的动点
AC,P是线段EF上的动点
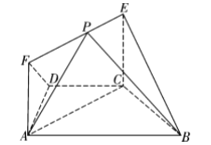
(1)求证:平面BCE⊥平面ACEF;
(2)求平面PAB与平面BCE所成锐二面角![]() 的最小值
的最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别是
,左、右焦点分别是![]() ,椭圆
,椭圆![]() 上短轴的一个端点与两个焦点构成的三角形的面积为
上短轴的一个端点与两个焦点构成的三角形的面积为![]() ;
;
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点(点
两点(点![]() 在第二象限),
在第二象限),![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点,若
两侧的动点,若![]() ,求证:直线
,求证:直线![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+x2,g(x)=xlna,a>1.
(1)求证:函数F(x)=f(x)-g(x)在(0,+∞)上单调递增;
(2)若函数y=![]() -3有四个零点,求b的取值范围;
-3有四个零点,求b的取值范围;
(3)若对于任意的x1,x2∈[-1,1]时,都有|F(x2)-F(x1)|≤e2-2恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市推行“共享汽车”服务,租用汽车按行驶里程加用车时间收费,标准是“1元/公里+0.2元/分钟”,刚在该市参加工作的小刘拟租用“共享汽车“上下班.单位同事老李告诉他:“上下班往返总路程虽然只有10公里,但偶尔上下班总共也需要用时大约1小时”,并将自己近50天往返开车的花费时间情况统计如下
时间(分钟) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
次数ξ | 8 | 18 | 14 | 8 | 2 |
将老李统计的各时间段频率视为相应概率,假定往返的路况不变,而且每次路上开车花费时间视为用车时间.
(1)试估计小刘每天平均支付的租车费用(每个时间段以中点时间计算);
(2)小刘认为只要上下班开车总用时不超过45分钟,租用“共享汽车”为他该日的“最优选择”,小刘拟租用该车上下班2天,设其中有ξ天为“最优选择”,求ξ的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com