
在R上可导的函数f(x)=![]() x3+
x3+![]() ax2+2bx+c,当x∈(0,1)时取得极大值,当x∈(1,2)时取得极小值,求点(a,b)对应的区域的面积以及
ax2+2bx+c,当x∈(0,1)时取得极大值,当x∈(1,2)时取得极小值,求点(a,b)对应的区域的面积以及![]() 的取值范围.
的取值范围.
![]()
![]()
函数f(x)的导数为f′(x)=x2+ax+2b,当x∈(0,1)时,f(x)取得极大值,当x∈(1,2)时,f(x)取得极小值,则方程x2+ax+2b=0有两个根,一个根在区间(0,1)内,另一个根在区间(1,2)内,由二次函数f′(x)=x2+ax+2b的图象与方程x2+ax+2b=0根的分布之间的关系可以得到
在aOb平面内作出满足约束条件的点(a,b)对应的区域为△ABD(不包括边界),
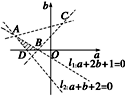 如图阴影部分,其中点A(-3,1),B(-1,0),D(-2,0),
如图阴影部分,其中点A(-3,1),B(-1,0),D(-2,0),
△ABD的面积为
S△ABD=![]() |BD|×h=
|BD|×h=![]() (h为点A到a轴的距离).
(h为点A到a轴的距离).
点C(1,2)与点(a,b)连线的斜率为![]() ,
,
显然![]()
![]() (kCA,kCB),
(kCA,kCB),
即![]()
![]()


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 2 |
| b-2 |
| a-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 2 |
| b-2 |
| a-1 |
A、(
| ||||
B、(
| ||||
C、(-
| ||||
D、(
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com