
【题目】已知函数f(x)=|3x﹣1|﹣2|x|+2.
(1)解不等式:f(x)<10;
(2)若对任意的实数x,f(x)﹣|x|≤a恒成立,求实数a的取值范围.
【答案】
(1)解:x<0时,不等式化为﹣3x+1+2x+2<10,解得x>﹣7,∴﹣7<x<0;
0 ![]() 时,不等式化为﹣3x+1﹣2x+2<10,解得x>﹣
时,不等式化为﹣3x+1﹣2x+2<10,解得x>﹣ ![]() ,∴0
,∴0 ![]() ;
;
x> ![]() 时,不等式化为3x﹣1﹣2x+2<10,解得x<9,∴
时,不等式化为3x﹣1﹣2x+2<10,解得x<9,∴ ![]() ;
;
综上所述,不等式的解集为(﹣7,9);
(2)解:对任意的实数x,f(x)﹣|x|≤a恒成立,即|3x﹣1|﹣|3x|≤a﹣2,
∵|3x﹣1|﹣|3x|≤|3x﹣1﹣3x|=1,
∴a﹣2≥1,∴a≥3.
【解析】(1)分类讨论,解不等式:f(x)<10;(2)对任意的实数x,f(x)﹣|x|≤a恒成立,即|3x﹣1|﹣|3x|≤a﹣2,利用|3x﹣1|﹣|3x|≤|3x﹣1﹣3x|=1,即可求实数a的取值范围.
【考点精析】解答此题的关键在于理解绝对值不等式的解法的相关知识,掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.


科目:高中数学 来源: 题型:
【题目】某城市100户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.

(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的平均数、众数和中位数;
(3)在月平均用电量为,![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在
的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC![]() BC,且AC=BC.
BC,且AC=BC.
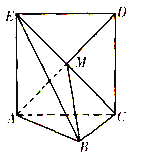
(1)求证:AM![]() 平面EBC;
平面EBC;
(2)求直线AB与平面EBC所成角的大小,
(3)求二面角A-BE-C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了政府对过热的房地产市场进行调控决策,统计部门对城市人和农村人进行了买房心理预测调研,用简单随机抽样的方法抽取了110人进行统计,得到如下列联表:
买房 | 不买房 | 纠结 | |
城市人 | 5 | 15 | |
农村人 | 20 | 10 |
已知样本中城市人数与农村人数之比是3:8.
(Ⅰ)分别求样本中城市人中的不买房人数和农村人中的纠结人数;
(Ⅱ)从参与调研的城市人中用分层抽样方法抽取6人,进一步统计城市人的某项收入指标,假设一个买房人的指标算作3,一个纠结人的指标算作2,一个不买房人的指标算作1,现在从这6人中再随机选取3人,令X=再抽取3人指标之和,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,其中前三段的频率成等比数列. 
(1)求图中实数a的值;
(2)若该校高一年级共有学生640人,试估计该校高一年级期中考试数学成绩不低于80分的人数;
(3)若从样本中数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,记这两名学生成绩在[90,100]内的人数为X,求随机变量X的分布列和期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若曲线f(x)= ![]() (e﹣1<x<e2﹣1)和g(x)=﹣x3+x2(x<0)上分别存在点A、B,使得△OAB是以原点O为直角顶点的直角三角形,且斜边AB的中点在y轴上,则实数a的取值范围是( )
(e﹣1<x<e2﹣1)和g(x)=﹣x3+x2(x<0)上分别存在点A、B,使得△OAB是以原点O为直角顶点的直角三角形,且斜边AB的中点在y轴上,则实数a的取值范围是( )
A.(e,e2)
B.(e, ![]() )
)
C.(1,e2)
D.[1,e)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=e2x , g(x)=kx+1(k∈R). (Ⅰ)若直线y=g(x)和函数y=f(x)的图象相切,求k的值;
(Ⅱ)当k>0时,若存在正实数m,使对任意x∈(0,m),都有|f(x)﹣g(x)|>2x恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥A﹣BCED中,AD⊥底面BCED,BD⊥DE,∠DBC=∠BCE═60°,BD=2CE. 
(1)若F是AD的中点,求证:EF∥平面ABC;
(2)若AD=DE,求BE与平面ACE所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com