
科目:高中数学 来源: 题型:
 ,70),[70,80),[80,90),[90,100].
,70),[70,80),[80,90),[90,100].| 分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| x:y | 5:4 | 1:1 | 3:5 | 5:1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 最新调查显示,目前我国主流城市白领亚健康的比例高达76%,处于过度疲劳状态的接近6成,大部分白领均缺乏运动锻炼.某健康协会为了了解白领们每天锻炼身体的时间(单位:分钟),进入一些国企中随机抽取了n名白领进行调查,其频率分布直方图如图所示,其中运动时间不低于20分钟的人数为81人,则n的值为
最新调查显示,目前我国主流城市白领亚健康的比例高达76%,处于过度疲劳状态的接近6成,大部分白领均缺乏运动锻炼.某健康协会为了了解白领们每天锻炼身体的时间(单位:分钟),进入一些国企中随机抽取了n名白领进行调查,其频率分布直方图如图所示,其中运动时间不低于20分钟的人数为81人,则n的值为查看答案和解析>>
科目:高中数学 来源: 题型:
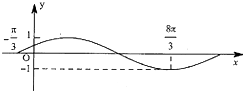 将函数y=sinx图象上点的横坐标扩大到原来的m倍,纵坐标保持不变,再向左平移n个单位得到如图所示函数的图象,则m,n可以为( )
将函数y=sinx图象上点的横坐标扩大到原来的m倍,纵坐标保持不变,再向左平移n个单位得到如图所示函数的图象,则m,n可以为( )A、m=2,n=
| ||
B、m=2,n=
| ||
C、m=4,n=
| ||
D、m=4,n=
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 1+x2 |
A、
| |||||||||||
B、
| |||||||||||
C、
| |||||||||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 6 |
| π |
| 6 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、ee | ||
| B、e2 | ||
| C、e | ||
D、e
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com