
��ѡ���⡿��A��B��C��D��С����ֻ��ѡ��������ÿС��l0�֣�����20�֣��������ָ�����������𣬽��ʱӦд������˵����֤�����̻����㲽�裮
A.ѡ��4 �C 1����֤��ѡ��
��ͼ����ABC�����Բ������AE��BC���ӳ����ཻ�ڵ�E,
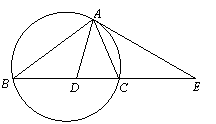 ��BAC��ƽ������BC���ڵ�D.
��BAC��ƽ������BC���ڵ�D.
��֤��ED2= EB��EC.
B��������任
��֪����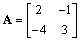 ��
��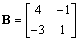 ��������
��������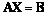 �Ķ�����
�Ķ�����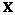 ��
��
C.ѡ��4 �C 4 ���������뼫����
���������ߵļ����귽�̷ֱ�Ϊr = 1��r = 2cos( + ),�����ཻ��A��B���㣬���߶�AB�ij�.
D.ѡ��4 �C 5 ����ʽ֤��ѡ��
��a,b,cΪ��ʵ��,��֤:a3 + b3 + c3 + ��2.
 ��ѡ���⡿��A��B��C��D��С����ֻ��ѡ��������ÿС��l0�֣�����20�֣��������ָ�����������𣬽��ʱӦд������˵����֤�����̻����㲽�裮
��ѡ���⡿��A��B��C��D��С����ֻ��ѡ��������ÿС��l0�֣�����20�֣��������ָ�����������𣬽��ʱӦд������˵����֤�����̻����㲽�裮
A.ѡ��4 �C 1����֤��ѡ��
֤��: ��ΪEA��Բ������,ACΪ���е�A����,����
ÐCAE = ÐCBA.
����ΪAD��ÐBAC��ƽ����,����ÐBAD = ÐCAD
����ÐDAE = ÐDAC + ÐEAC = ÐBAD + ÐCBA = ÐADE
����,��EAD�ǵ���������,����EA = ED. ����������������������������������������6��
��EA2 = EC��EB,
����ED2 = EB��EC. ����������������������������������������������������������4��
B��������任��
�⣺�������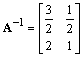 ����������������������������������������5��
����������������������������������������5��
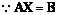 ��
��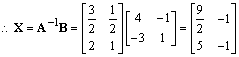 ������������������������������10��
������������������������������10��
C.ѡ��4 �C 4 ���������뼫����
���������ߵļ����귽�̷ֱ�Ϊr = 1��r = 2cos( + ),�����ཻ��A,B����,���߶�AB�ij�.
�� ���Ƚ������ߵļ����귽�̻�Ϊֱ�����귽��,��
x2 + y2 = 1��x2 + y2 �C x + y = 0����������������������������������������6��
�ⷽ���������������(1,0),(�C, �C )
����,�߶�AB�ij�Ϊ=
��AB = .������������������������������������������������������������10��
D.ѡ��4 �C 5 ����ʽ֤��ѡ��
��a,b,cΪ��ʵ��,��֤:a3 + b3 + c3 + ��2.
֤�� ��Ϊa,b,cΪ��ʵ��,����a3 + b3 + c3��3 = 3abc>0��������������������5��
��3abc + ��2 = 2.
����a3 + b3 + c3 + ��2.��������������������������������������������������10��


 �ǻ�С��ϰϵ�д�
�ǻ�С��ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x2 |
| 4 |
| y2 |
| 9 |
| �� |
| 2 |
| �� |
| 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ѡ���⡿��A��B��C��D��С����ֻ��ѡ��2�⣬ÿС��10�֣�����20�֣����ڴ��ָ�����������𣮽��Ӧд������˵����֤�����̻����㲽�裮
��ѡ���⡿��A��B��C��D��С����ֻ��ѡ��2�⣬ÿС��10�֣�����20�֣����ڴ��ָ�����������𣮽��Ӧд������˵����֤�����̻����㲽�裮
|
| �� |
| 4 |
| 2 |
|
| x |
| yz |
| y |
| zx |
| z |
| xy |
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ѡ���⡿��A��B��C��D��С����ֻ��ѡ��������ÿС��l0�֣�����20�֣��������ָ�����������𣬽��ʱӦд������˵����֤�����̻����㲽�裮
A.ѡ��4 �C 1����֤��ѡ��
��ͼ����ABC�����Բ������AE��BC���ӳ����ཻ�ڵ�E,
 ��BAC��ƽ������BC���ڵ�D.
��BAC��ƽ������BC���ڵ�D.
��֤��ED2= EB��EC.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012-2013ѧ�꽭��ʡ��ͨ�к�����ѧ�������ϣ���ѧ�����ѧ�Ծ��������棩 ���ͣ������
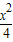 +
+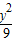 =1��M-1�������µ������ߵķ��̣�
=1��M-1�������µ������ߵķ��̣� ������ֱ��l����P������б��Ϊ
������ֱ��l����P������б��Ϊ 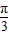 ��ԲC��MΪԲ�ġ�4Ϊ�뾶��
��ԲC��MΪԲ�ġ�4Ϊ�뾶���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com