
【题目】已知函数![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)求函数![]() 的极值;
的极值;
(2)问:是否存在实数![]() ,使得
,使得![]() 有两个相异零点?若存在,求出
有两个相异零点?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(1) ①当![]() 时,函数
时,函数![]() 无极值.②当
无极值.②当![]() 时,函数
时,函数![]() 有极小值为
有极小值为![]() ,无极大值;(2)存在,
,无极大值;(2)存在,![]()
【解析】
(1)对函数![]() 求导,根据
求导,根据![]() 的不同取值范围,进行分类讨论,求出函数
的不同取值范围,进行分类讨论,求出函数![]() 的极值;
的极值;
(2)根据![]() 的不同取值范围,进行分类讨论,结合
的不同取值范围,进行分类讨论,结合![]() 、函数的极值的大小、(1)中的结论,最后求出
、函数的极值的大小、(1)中的结论,最后求出![]() 的取值范围.
的取值范围.
解:(1)因为![]() ,所以
,所以![]() .
.
①当![]() 时,
时,![]() ,
,
所以![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递减.
上单调递减.
此时,函数![]() 无极值.
无极值.
②当![]() 时,令
时,令![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增.
上单调递增.
此时,函数![]() 有极小值为
有极小值为![]() ,无极大值.
,无极大值.
(2)存在实数![]() ,使得
,使得![]() 有两个相异零点.
有两个相异零点.
由(1)知:①当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减;
上单调递减;
又![]() ,所以此时函数
,所以此时函数![]() 仅有一个零点;
仅有一个零点;
②当![]() 时,
时,![]() .
.
因为![]() ,则由(1)知
,则由(1)知![]() ;
;
取![]() ,令
,令![]() ,
,
易得![]() ,所以
,所以![]() 在
在![]() 单调递减,
单调递减,
所以![]() ,所以
,所以![]() .
.
此时,函数![]() 在
在![]() 上也有一个零点.
上也有一个零点.
所以,当![]() 时,函数
时,函数![]() 有两个相异零点.
有两个相异零点.
③当![]() 时,
时,![]() ,
,![]() ,
,
此时函数![]() 仅有一个零点.
仅有一个零点.
④当![]() 时,
时,![]() ,因为
,因为![]() ,则由(1)知
,则由(1)知![]() ;
;
令函数![]() ,易得
,易得![]() ,
,
所以![]() ,所以
,所以![]() ,即
,即![]() .
.
又![]() ,所以函数
,所以函数![]() 在
在![]() 上也有一个零点,
上也有一个零点,
所以,当![]() 时,函数
时,函数![]() 有两个相异零点.
有两个相异零点.
综上所述,当![]() 时,函数
时,函数![]() 有两个相异零点.
有两个相异零点.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,经过点
,经过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在等腰![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点,![]() 在线段
在线段![]() 上,且
上,且![]() 。将
。将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到
到![]() 的位置(如图2所示),且
的位置(如图2所示),且![]() 。
。
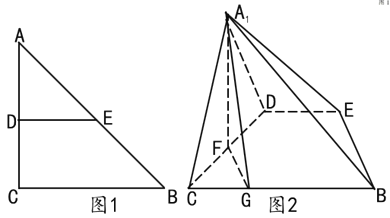
(1)证明:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值
所成锐二面角的余弦值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() 满足约束条件
满足约束条件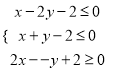 ,若
,若![]() 取得最大值的最优解不唯一,则实数
取得最大值的最优解不唯一,则实数![]() 的值为__________.
的值为__________.
【答案】![]() 或
或![]()
【解析】由题可知若![]() 取得最大值的最优解不唯一则
取得最大值的最优解不唯一则![]() 必平行于可行域的某一边界,如图:
必平行于可行域的某一边界,如图: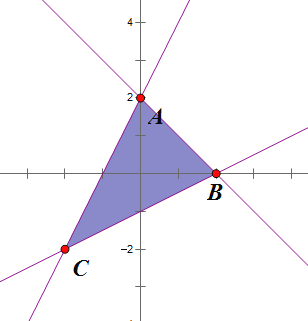 要Z最大则直线与y轴的截距最大即可,当a<0时,则平行AC直线即可故a=-2,当a>0时,则直线平行AB即可,故a=1
要Z最大则直线与y轴的截距最大即可,当a<0时,则平行AC直线即可故a=-2,当a>0时,则直线平行AB即可,故a=1
点睛:线性规划为常考题型,解决此题务必要理解最优解个数为无数个时的条件是什么,然后根据几何关系求解即可
【题型】填空题
【结束】
16
【题目】《数书九章》三斜求积术:“以小斜幂,并大斜幂,减中斜幂,余半之,自乘于上;以小斜幂乘大斜幂,减上,余四约一,为实,一为从隅,开平方得积”.秦九韶把三角形的三条边分别称为小斜、中斜和大斜,“术”即方法.以![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别表示三角形的面积,大斜,中斜,小斜;
分别表示三角形的面积,大斜,中斜,小斜; ![]() ,
, ![]() ,
, ![]() 分别为对应的大斜,中斜,小斜上的高;则
分别为对应的大斜,中斜,小斜上的高;则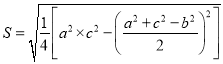
![]()
![]() .若在
.若在![]() 中
中![]() ,
, ![]() ,
, ![]() ,根据上述公式,可以推出该三角形外接圆的半径为__________.
,根据上述公式,可以推出该三角形外接圆的半径为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]()
(![]() )求数列
)求数列![]() 的通项公式;
的通项公式;
(![]() )若数列
)若数列![]() 满足
满足![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(![]() )在(
)在(![]() )的条件下,设
)的条件下,设![]() ,问是否存在实数
,问是否存在实数![]() 使得数列
使得数列![]() 是单调递增数列?若存在,求出
是单调递增数列?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某制药厂准备投入适当的广告费,对产品进行宣传,在一年内,预计年销量Q(万件)与广告费x(万元)之间的函数关系为Q![]() (x≥0).已知生产此产品的年固定投入为3万元,每生产1万件此产品仍需后期再投入32万元,若每件售价为“年平均每件投入的150%”与“年平均每件所占广告费的50%”之和(注:投入包括“年固定投入”与“后期再投入”).
(x≥0).已知生产此产品的年固定投入为3万元,每生产1万件此产品仍需后期再投入32万元,若每件售价为“年平均每件投入的150%”与“年平均每件所占广告费的50%”之和(注:投入包括“年固定投入”与“后期再投入”).
(1)试将年利润w万元表示为年广告费x万元的函数,并判断当年广告费投入100万元时,企业亏损还是盈利?
(2)当年广告费投入多少万元时,企业年利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校数学建模小组为了研究双层玻璃窗户中每层玻璃厚度![]() (每层玻璃的厚度相同)及两层玻璃间夹空气层厚度
(每层玻璃的厚度相同)及两层玻璃间夹空气层厚度![]() 对保温效果的影响,利用热传导定律得到热传导量
对保温效果的影响,利用热传导定律得到热传导量![]() 满足关系式:
满足关系式: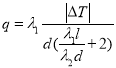 ,其中玻璃的热传导系数
,其中玻璃的热传导系数![]() 焦耳/(厘米
焦耳/(厘米![]() 度),不流通、干燥空气的热传导系数
度),不流通、干燥空气的热传导系数![]() 焦耳/(厘米
焦耳/(厘米![]() 度),
度), ![]() 为室内外温度差.
为室内外温度差.![]() 值越小,保温效果越好.现有4种型号的双层玻璃窗户,具体数据如下表:
值越小,保温效果越好.现有4种型号的双层玻璃窗户,具体数据如下表:
型号 | 每层玻璃厚度 (单位:厘米) | 玻璃间夹空气层厚度 (单位:厘米) |
A型 |
|
|
B型 |
|
|
C型 |
|
|
D型 |
|
|
则保温效果最好的双层玻璃的型号是________型.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方体![]() 的棱长为
的棱长为![]() ,点
,点![]() 为棱
为棱![]() 的中点.下列结论:①线段
的中点.下列结论:①线段![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ;②线段
;②线段![]() 上存在点
上存在点![]() ,使
,使![]() 得平面
得平面![]() ;③平面
;③平面![]() 把正方体分成两部分,较小部分的体积为
把正方体分成两部分,较小部分的体积为![]() ,其中所有正确的序号是( )
,其中所有正确的序号是( )
A.①B.③C.①③D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 的值域;
的值域;
(2)当![]() 时,求
时,求![]() 的最小值
的最小值![]() ;
;
(3)是否存在实数![]() 、
、![]() ,同时满足下列条件:①
,同时满足下列条件:① ![]() ;② 当
;② 当![]() 的定义域为
的定义域为![]() 时,其值域为
时,其值域为![]() .若存在,求出
.若存在,求出![]() 、
、![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com