
分析 (1)通过抛物线C方程可知F(0,4),从而可设直线l方程为y-4=kx,并与抛物线方程联立可知x1+x2=16k、x1x2=-64,进而化简计算即得结论;
(2)取定点Q(0,-4),则tan∠AQF=$\frac{-16{x}_{1}}{64+{{x}_{1}}^{2}}$、tan∠BQF=$\frac{16{x}_{2}}{{{x}_{2}}^{2}+64}$,通过(1)代入x1x2=-64化简,计算即得结论.
解答 解:(1)∵抛物线C:x2=16y,
∴F(0,4),
依题意可知直线l的斜率k存在,设直线l方程为:y-4=kx,
联立直线与抛物线方程,消去y整理得:x2-16kx-64=0,
设A(x1,y1),B(x2,y2),
由韦达定理可知:x1+x2=16k,x1x2=-64,
则$\frac{1}{y_1}+\frac{1}{y_2}$=16($\frac{1}{{{x}_{1}}^{2}}$+$\frac{1}{{{x}_{2}}^{2}}$)=16•$\frac{({x}_{1}+{x}_{2})^{2}-2{x}_{1}{x}_{2}}{{(x}_{1}{x}_{2})^{2}}$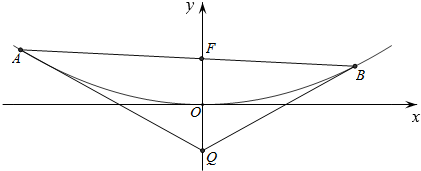
=$\frac{16[(16k)^{2}-2•(-64)]}{(-64)^{2}}$=k2+$\frac{1}{2}$>$\frac{1}{2}$,
即$\frac{1}{y_1}+\frac{1}{y_2}$的取值范围是:($\frac{1}{2}$,+∞);
(2)结论:存在定点Q(0,-4),使得无论AB怎样运动都有∠AQF=∠BQF.
理由如下:
由(1)可知:x1+x2=16k,x1x2=-64,
则tan∠AQF=$\frac{{0-x}_{1}}{{y}_{1}-(-4)}$=$\frac{-{x}_{1}}{4+\frac{{{x}_{1}}^{2}}{16}}$=$\frac{-16{x}_{1}}{64+{{x}_{1}}^{2}}$=$\frac{-16{x}_{1}}{{{x}_{1}}^{2}-{x}_{1}{x}_{2}}$=$\frac{-16}{{x}_{1}-{x}_{2}}$,
tan∠BQF=$\frac{{x}_{2}-0}{{y}_{2}-(-4)}$=$\frac{{x}_{2}}{\frac{{{x}_{2}}^{2}}{16}+4}$=$\frac{16{x}_{2}}{{{x}_{2}}^{2}-{x}_{1}{x}_{2}}$=$\frac{16}{{x}_{2}-{x}_{1}}$,
∴tan∠AQF=tan∠BQF,即无论AB怎样运动都有∠AQF=∠BQF.
点评 本题考查直线与圆锥曲线的关系,考查数形结合能力,注意解题方法的积累,属于中档题.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{5}{6}$ | C. | 2 | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
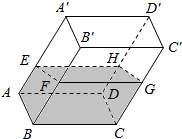 如图,在透明塑料制成的长方体ABCD-A′B′C′D′容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:
如图,在透明塑料制成的长方体ABCD-A′B′C′D′容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
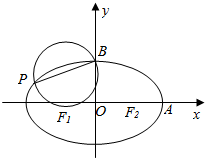 设椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点为F1,F2,右顶点为A,上顶点为B.已知|AB|=$\frac{\sqrt{3}}{2}$|F1F2|.
设椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点为F1,F2,右顶点为A,上顶点为B.已知|AB|=$\frac{\sqrt{3}}{2}$|F1F2|.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
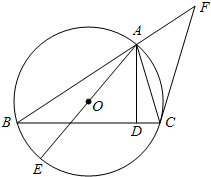 如图,已知⊙O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是⊙O的直径.
如图,已知⊙O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是⊙O的直径.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{4\sqrt{3}}{3}$ | C. | 2 | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com