
【题目】如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=2,E、F分别为BC、AD的中点,点M在线段PD上.
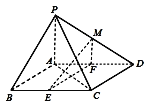
(1)求证:EF⊥平面PAC;
(2)如果直线ME与平面PBC所成的角和直线ME与平
面ABCD所成的角相等,求![]() 的值.
的值.
【答案】(1)见解析;(2) ![]() .
.
【解析】试题分析: ![]() 由平行四边形的性质可得
由平行四边形的性质可得![]() ,即
,即![]() ,由面面垂直的性质得出
,由面面垂直的性质得出![]() 平面
平面![]() ,故
,故![]() ,从而
,从而![]() 平面
平面![]()
![]() 以
以![]() 为原点建立空间直角坐标系,设
为原点建立空间直角坐标系,设![]() ,
, ![]() ,求出平面
,求出平面![]() ,平面
,平面![]() 的法向量
的法向量![]() 以及
以及![]() 的坐标,根据线面角相等列方程求解即可得到答案
的坐标,根据线面角相等列方程求解即可得到答案
解析:(1)证明:在平行四边形![]() 中,因为
中,因为![]() ,
,![]() ,
,
所以![]() .由
.由![]() 分别为
分别为![]() 的中点,得
的中点,得![]() , 所以
, 所以![]() .
.
因为侧面![]() 底面
底面![]() ,且
,且![]() ,所以
,所以![]() 底面
底面![]() .
.
又因为![]() 底面
底面![]() ,所以
,所以![]() .
.
又因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)解:因为![]() 底面
底面![]() ,
,![]() ,所以
,所以![]() 两两
两两
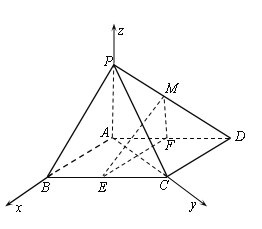
垂直,以![]() 分别为
分别为![]() 、
、![]() 、
、![]() ,建立空间直角坐标系,则
,建立空间直角坐标系,则
![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,
所以![]() ,
,![]() ,易得平面
,易得平面
![]() 的法向量
的法向量![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,由
,由![]() ,
,![]() ,得
,得![]() 令
令![]() , 得
, 得![]() .
.
因为直线![]() 与平面
与平面![]() 所成的角和此直线与平面
所成的角和此直线与平面![]() 所成的角相等,
所成的角相等,
所以![]() ,即
,即![]() ,所以
,所以 ![]() ,
,
解得![]() ,或
,或![]() (舍). 综上所得:
(舍). 综上所得:![]()


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其最小正周期为
,其最小正周期为![]() .
.
(1)求![]() 的表达式;
的表达式;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度后,再将得到的图象上各点的横坐标伸长到原来的
个单位长度后,再将得到的图象上各点的横坐标伸长到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象,若关于
的图象,若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有且只有一个实数解,求实数
上有且只有一个实数解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() ,侧面
,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
, ![]() 分别为
分别为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)如果直线![]() 与平面
与平面![]() 所成的角和直线
所成的角和直线![]() 与平面
与平面![]() 所成的角相等,求
所成的角相等,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下表格记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以![]() 表示.
表示.
甲组 | 9 | 9 | 11 | 11 |
乙组 |
| 8 | 9 | 10 |
(1)如果![]() ,求乙组同学植树棵数的平均数和方差;
,求乙组同学植树棵数的平均数和方差;
(2)如果![]() ,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率.
,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】取数游戏:每次游戏中,游戏人按动游泳按钮,就从如图:![]() 的三个窗口中各弹出一个数字,其中:最左边窗口可随机弹出数字4或3,中间窗口可随机弹出3或2,最右边窗口可随机弹出2或1.若弹出的三个数字为“顺子”(如:432),则可获奖10元,若有相邻两位数字相同,则可获奖8元,其他情况获奖-2元.甲玩了8次游戏后,乙问甲的获奖情况,甲说:“23元有余,28元不足,3除不尽.”那么甲在这8次游戏中得到“顺子”、“相邻两位数字相同”、“其他情况”的次数依次为( )
的三个窗口中各弹出一个数字,其中:最左边窗口可随机弹出数字4或3,中间窗口可随机弹出3或2,最右边窗口可随机弹出2或1.若弹出的三个数字为“顺子”(如:432),则可获奖10元,若有相邻两位数字相同,则可获奖8元,其他情况获奖-2元.甲玩了8次游戏后,乙问甲的获奖情况,甲说:“23元有余,28元不足,3除不尽.”那么甲在这8次游戏中得到“顺子”、“相邻两位数字相同”、“其他情况”的次数依次为( )
A. 0,4,4 B. 2,2,4 C. 2,3,3 D. 1,3,4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称.某市为了了解人们对“一带一路”的认知程度,对不同年龄和不同职业的人举办了一次“一带一路”知识竞赛,满分100分(90分及以上为认知程度高).现从参赛者中抽取了![]() 人,按年龄分成5组,第一组:
人,按年龄分成5组,第一组: ![]() ,第二组:
,第二组: ![]() ,第三组:
,第三组: ![]() ,第四组:
,第四组: ![]() ,第五组:
,第五组: ![]() ,得到如图所示的频率分布直方图,已知第一组有6人.
,得到如图所示的频率分布直方图,已知第一组有6人.
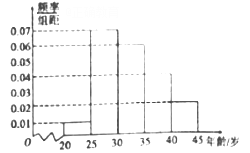
(1)求![]() ;
;
(2)求抽取的![]() 人的年龄的中位数(结果保留整数);
人的年龄的中位数(结果保留整数);
(3)从该市大学生、军人、医务人员、工人、个体户 五种人中用分层抽样的方法依次抽取6人,42人,36人,24人,12人,分别记为1~5组,从这5个按年龄分的组和5个按职业分的组中每组各选派1人参加知识竞赛,分别代表相应组的成绩,年龄组中1~5组的成绩分别为93,96,97,94,90,职业组中1~5组的成绩分别为93,98,94,95,90.
(Ⅰ)分别求5个年龄组和5个职业组成绩的平均数和方差;
(Ⅱ)以上述数据为依据,评价5个年龄组和5个职业组对“一带一路”的认知程度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com