
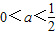 或
或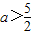 .因为“P∨Q”为真且“P∧Q”为假,说明命题P、Q中一个为真,另一个为假,最后据此进行分类讨论,可得a的取值范围.
.因为“P∨Q”为真且“P∧Q”为假,说明命题P、Q中一个为真,另一个为假,最后据此进行分类讨论,可得a的取值范围.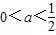 或
或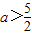 …(4分)
…(4分) ⇒
⇒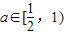 …(9分)
…(9分) ,⇒
,⇒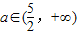 …(12分)
…(12分)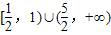 …(14分)
…(14分)

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2007-2008学年广东省华南师大附中高三综合测试数学试卷3(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com