
分析 (1)由题意知ξ的可能取值为0,1,2,分别求出相应的概率,由此能求出ξ的分布列.
(2)由题意知η的可能取值为0,1,2,3,且~B(3,$\frac{1}{3}$),由此能求出η的分布列.
解答 解:(1)由题意知ξ的可能取值为0,1,2,
P(ξ=0)=$\frac{{C}_{4}^{3}}{{C}_{6}^{3}}$=$\frac{1}{5}$,
P(ξ=1)=$\frac{{C}_{4}^{2}{C}_{2}^{1}}{{C}_{6}^{3}}$=$\frac{3}{5}$,
P(ξ=2)=$\frac{{C}_{4}^{1}{C}_{2}^{2}}{{C}_{6}^{3}}$=$\frac{1}{5}$,
∴ξ的分布列为:
| ξ | 0 | 1 | 2 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
| η | 0 | 1 | 2 | 3 |
| P | $\frac{8}{27}$ | $\frac{4}{9}$ | $\frac{2}{9}$ | $\frac{1}{27}$ |
点评 本题考查离散型随机变量的分布列的求法,考查推理论证能力、运算求解能力,考查等价转化思想,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
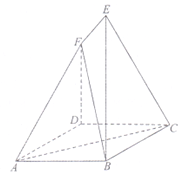 如图,ABCD是边长为a的菱形,∠BAD=60°,EB⊥平面ABCD,FD⊥平面ABCD,EB=2FD=$\sqrt{3}$a
如图,ABCD是边长为a的菱形,∠BAD=60°,EB⊥平面ABCD,FD⊥平面ABCD,EB=2FD=$\sqrt{3}$a查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({3\sqrt{2},\frac{3π}{4}})$ | B. | $({3\sqrt{2},\frac{5π}{4}})$ | C. | $({3,\frac{5π}{4}})$ | D. | $({3,\frac{3π}{4}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-2,-1,0,1,2} | B. | {-1,2,3} | C. | {-2,-1,0,1,2,3} | D. | {-1,2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com