
【题目】已知函数![]() .
.
⑴从区间![]() 内任取一个实数
内任取一个实数![]() ,设事件
,设事件![]() 表示“函数
表示“函数![]() 在区间
在区间![]() 上有两个不同的零点”,求事件
上有两个不同的零点”,求事件![]() 发生的概率;
发生的概率;
⑵若联系掷两次一颗均匀的骰子(骰子六个面上标注的点数分别为![]() )得到的点数分别为
)得到的点数分别为![]() 和
和![]() ,记事件
,记事件![]() 表示“
表示“![]() 在
在![]() 上恒成立”,求事件
上恒成立”,求事件![]() 发生的概率.
发生的概率.
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() ,若不等式
,若不等式![]() 的解集为(1,4),且方程f(x)=x有两个相等的实数根。
的解集为(1,4),且方程f(x)=x有两个相等的实数根。
(1)求f(x)的解析式;
(2)若不等式f(x)>mx在![]() 上恒成立,求实数m的取值范围;
上恒成立,求实数m的取值范围;
(3)解不等式![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() 为椭圆上一点(在
为椭圆上一点(在![]() 轴上方),连结
轴上方),连结![]() 并延长交椭圆于另一点
并延长交椭圆于另一点![]() ,设
,设![]() .
.

(1)若点![]() 的坐标为
的坐标为![]() ,且
,且![]() 的周长为8,求椭圆
的周长为8,求椭圆![]() 的方程;
的方程;
(2)若![]() 垂直于
垂直于![]() 轴,且椭圆
轴,且椭圆![]() 的离心率
的离心率![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运输队接到给灾区运送物资的任务,该运输队有8辆载重为![]() 的
的![]() 型卡车,6辆载重为
型卡车,6辆载重为![]() 的
的![]() 型卡车,10名驾驶员,要求此运输队每天至少运送
型卡车,10名驾驶员,要求此运输队每天至少运送![]() 救灾物资.已知每辆卡车每天往返的次数为
救灾物资.已知每辆卡车每天往返的次数为![]() 型卡车16次,
型卡车16次, ![]() 型卡车12次.每辆卡车每天往返的成本为
型卡车12次.每辆卡车每天往返的成本为![]() 型卡车240元,
型卡车240元, ![]() 型卡车378元.问每天派出
型卡车378元.问每天派出![]() 型卡车与
型卡车与![]() 型卡车各多少辆,运输队所花的成本最低?
型卡车各多少辆,运输队所花的成本最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() ,直线
,直线![]() ,过右焦点
,过右焦点![]() 的直线与椭圆交于
的直线与椭圆交于![]() 两点,线段
两点,线段![]() 的垂直平分线分别交直线
的垂直平分线分别交直线![]() 和
和![]() 于点
于点![]() .
.
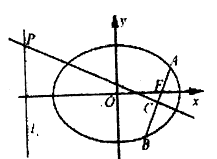
(1)求弦长![]() 的最小值;
的最小值;
(2)在直线![]() 上任取一点
上任取一点![]() ,当
,当![]() 的斜率
的斜率![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com