
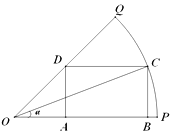
【题目】某园林公司准备绿化一块半径为200米,圆心角为 ![]() 的扇形空地(如图的扇形OPQ区域),扇形的内接矩形ABCD为一水池,其余的地方种花,若∠COP=α,矩形ABCD的面积为S(单位:平方米).
的扇形空地(如图的扇形OPQ区域),扇形的内接矩形ABCD为一水池,其余的地方种花,若∠COP=α,矩形ABCD的面积为S(单位:平方米). 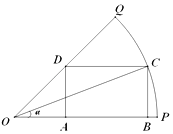
(1)试将S表示为关于α的函数,求出该函数的表达式;
(2)角α取何值时,水池的面积 S最大,并求出这个最大面积.
【答案】
(1)解:在Rt△OBC中,OB=200cosα,BC=200sinα ![]()
在Rt△OAD中, ![]() ,
,
∴OA=DA=BC=200sinα
∴AB=OB﹣OA=200cosα﹣200sinα,
故S=ABBC=(200cosα﹣200sinα)200sinα
=40000sinαcosα﹣40000sin2α=20000sin2α﹣20000(1﹣cos2α)
=20000(sin2α+cos2α)﹣20000
= ![]() ,
, ![]()
(2)解:由 ![]() ,得
,得 ![]() ,
,
所以当 ![]() ,即
,即 ![]() 时,
时,
S最大= ![]()
因此,当 ![]() 时,水池的面积S最大,最大面积为
时,水池的面积S最大,最大面积为 ![]() 平方米
平方米
【解析】(1)在Rt△OBC中,OB=200cosα,BC=200sinα ![]() ,求出BC=200sinα,AB=200cosα﹣200sinα,得到S=
,求出BC=200sinα,AB=200cosα﹣200sinα,得到S= ![]() ,
, ![]() 即可.(2)利用三角函数的最值,求解
即可.(2)利用三角函数的最值,求解 ![]() 时,水池的面积S最大,最大面积为
时,水池的面积S最大,最大面积为 ![]() 平方米.
平方米.


 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:
【题目】在极坐标系中,圆![]() 的极坐标方程为
的极坐标方程为![]() ,若以极点
,若以极点![]() 为原点,极轴所在的直线为
为原点,极轴所在的直线为![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(1)求圆![]() 的参数方程;
的参数方程;
(2)在直线坐标系中,点![]() 是圆
是圆![]() 上的动点,试求
上的动点,试求![]() 的最大值,并求出此时点
的最大值,并求出此时点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下命题中,正确命题的序号是 . ①函数y=tanx在定义域内是增函数;
②函数y=2sin(2x+ ![]() )的图象关于x=
)的图象关于x= ![]() 成轴对称;
成轴对称;
③已知 ![]() =(3,4),
=(3,4), ![]()
![]() =﹣2,则向量
=﹣2,则向量 ![]() 在向量
在向量 ![]() 的方向上的投影是﹣
的方向上的投影是﹣ ![]()
④如果函数f(x)=ax2﹣2x﹣3在区间(﹣∞,4)上是单调递减的,则实数a的取值范围是(0, ![]() ].
].
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将边长为![]() 的等边
的等边![]() 沿
沿![]() 轴正方向滚动,某时刻
轴正方向滚动,某时刻![]() 与坐标原点重合(如图),设顶点
与坐标原点重合(如图),设顶点![]() 的轨迹方程是
的轨迹方程是![]() ,关于函数
,关于函数![]() 有下列说法:
有下列说法:

(1)![]() 的值域为
的值域为![]() ;
;
(2)![]() 是周期函数且周期为
是周期函数且周期为![]() ;
;
(3)![]() ;
;
(4)滚动后,当顶点![]() 第一次落在
第一次落在![]() 轴上时,
轴上时,![]() 的图象与
的图象与![]() 轴所围成的面积为
轴所围成的面积为![]()
其中正确命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为得到函数 ![]() 的图象,只需将函数y=sin2x的图象( )
的图象,只需将函数y=sin2x的图象( )
A.向左平移 ![]() 个长度单位
个长度单位
B.向右平移 ![]() 个长度单位
个长度单位
C.向左平移 ![]() 个长度单位
个长度单位
D.向右平移 ![]() 个长度单位
个长度单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,且当x≥0时,f(x)=x|x﹣2|.若关于x的方程f2(x)+af(x)+b=0(a,b∈R)恰有10个不同实数解,则a的取值范围为( )
A.(0,2)
B.(﹣2,0)
C.(1,2)
D.(﹣2,﹣1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是由
是由![]() 个有序实数构成的一个数组,记作
个有序实数构成的一个数组,记作![]() ,其中
,其中![]()
![]()
![]() 称为数组
称为数组![]() 的“元”,
的“元”, ![]() 称为
称为![]() 的下标,如果数组
的下标,如果数组![]() 中的每个“元”都是来自数组
中的每个“元”都是来自数组
![]() 中不同下标的“元”,则称
中不同下标的“元”,则称![]() 为
为![]() 的子数组,定义两个数组
的子数组,定义两个数组![]() 和
和![]()
![]() 的关系数为
的关系数为![]() ;
;
(1)若![]() ,
, ![]() ,设
,设![]() 是
是![]() 的含有两个“元”的子数组,求
的含有两个“元”的子数组,求![]()
的最大值;
(2)若 ,
, ![]() ,且
,且![]() ,
, ![]() 为
为![]() 的含有三个“元”
的含有三个“元”
的子数组,求![]() 的最大值;
的最大值;
(3)若数组![]() 中的“元”满足
中的“元”满足![]() ,设数组
,设数组![]()
![]() 含有
含有
四个“元”![]() ,且
,且![]() ,求
,求![]() 与
与![]() 的所有含有三个“元”
的所有含有三个“元”
的子数组的关系数的最大值;
查看答案和解析>>
科目:高中数学 来源: 题型:
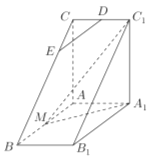
【题目】如图,直三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点,△
的中点,△![]() 是等腰三角形,
是等腰三角形, ![]() 为
为![]() 的中点,
的中点, ![]() 为
为![]() 上一点;
上一点;
(1)若![]() ∥平面
∥平面![]() ,求
,求![]() ;
;
(2)平面![]() 将三棱柱
将三棱柱![]() 分成两个部分,求含有点
分成两个部分,求含有点![]() 的那部分体积;
的那部分体积;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com