
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() .
.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求证: ![]() 平面
平面![]() ;
;
(3)若![]() 是
是![]() 的中点,求三棱锥
的中点,求三棱锥![]() 的体积.
的体积.
【答案】(1)详见解析;(2)详见解析;(3)![]() .
.
【解析】试题分析:(1)根据线面平行的判定,只需证明直线![]() 与平面
与平面![]() 上的某一条直线平行即可,而条件中直接给出了
上的某一条直线平行即可,而条件中直接给出了![]() ,因此结合线面平行的判定,可直接证明
,因此结合线面平行的判定,可直接证明![]() 平面
平面![]() ;(2)首先根据条件中给出的数据易得
;(2)首先根据条件中给出的数据易得![]() ,从而根据勾股定理可得
,从而根据勾股定理可得![]() ,再由条件
,再由条件![]() 平面
平面![]() 可得
可得![]() ,从而根据线面垂直的判定即可证得
,从而根据线面垂直的判定即可证得![]() 平面
平面![]() ;(3)由
;(3)由![]() 是
是![]() 即可得
即可得![]() 到面
到面![]() 的距离是
的距离是![]() 到面
到面![]() 距离的一半,从而
距离的一半,从而![]() .
.
试题解析:(1)∵![]() ,且
,且![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ; 4分
; 4分
(2)在直角梯形![]() 中,过
中,过![]() 作
作![]() 于点
于点![]() ,则四边形
,则四边形![]() 为矩形,
为矩形,
∴![]() ,又∵
,又∵![]() ,∴
,∴![]() ,在
,在![]() 中,
中,![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() ,则
,则![]() ,
,
∴![]() ,∴
,∴![]() , 8分
, 8分
又∵![]() 平面
平面![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() ; 10分
; 10分
(3)∵![]() 是
是![]() 中点,∴
中点,∴![]() 到面
到面![]() 的距离是
的距离是![]() 到面
到面![]() 距离的一半,
距离的一半,
∴![]() . 14分
. 14分


科目:高中数学 来源: 题型:
【题目】响应“文化强国建设”号召,某市把社区图书阅览室建设增列为重要的民生工程.为了解市民阅读需求,随机抽取市民200人做调查,统计显示,男士喜欢阅读古典文学的有64人,不喜欢的有56人;女士喜欢阅读古典文学的有36人,不喜欢的有44人.
(1)能否在犯错误的概率不超过0.25的前提下认为喜欢阅读古典文学与性别有关系?
(2)为引导市民积极参与阅读,有关部门牵头举办市读书交流会,从这200人中筛选出5名男代表和4名代表,其中有3名男代表和2名女代表喜欢古典文学.现从这9名代表中任选3名男代表和2名女代表参加交流会,记![]() 为参加交流会的5人中喜欢古典文学的人数,求
为参加交流会的5人中喜欢古典文学的人数,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
附:![]() ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(附加题,本小题满分10分,该题计入总分)
已知函数![]() ,若在区间
,若在区间![]() 内有且仅有一个
内有且仅有一个![]() ,使得
,使得![]() 成立,则称函数
成立,则称函数![]() 具有性质
具有性质![]() .
.
(1)若![]() ,判断
,判断![]() 是否具有性质
是否具有性质![]() ,说明理由;
,说明理由;
(2)若函数![]() 具有性质
具有性质![]() ,试求实数
,试求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方体![]() 的棱长为1,线段
的棱长为1,线段![]() 上有两个动点
上有两个动点![]() ,且
,且![]() ,则下列结论中正确的是__________.
,则下列结论中正确的是__________.
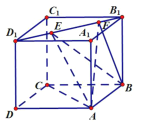
①![]() 平面
平面![]() ;
;
②平面![]() 平面
平面![]() ;
;
③三棱锥![]() 的体积为定值;
的体积为定值;
④存在某个位置使得异面直线![]() 与
与![]() 成角
成角![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,点
,点 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,使得
两点,使得![]()
![]() 是椭圆的左焦点
是椭圆的左焦点![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 满足:①圆心在第一象限,截
满足:①圆心在第一象限,截![]() 轴所得弦长为2;②被
轴所得弦长为2;②被![]() 轴分成两段圆弧,其弧长的比为
轴分成两段圆弧,其弧长的比为![]() ;③圆心到直线
;③圆心到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)求圆![]() 的方程;
的方程;
(Ⅱ)若点![]() 是直线
是直线![]() 上的动点,过点
上的动点,过点![]() 分别做圆
分别做圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,
, ![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C经过点(3,6)且焦点在x轴上.
(1)求抛物线C的标准方程;
(2)直线l: ![]() 过抛物线C的焦点F且与抛物线C交于A,B两点,求A,B两点间的距离.
过抛物线C的焦点F且与抛物线C交于A,B两点,求A,B两点间的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1,AC⊥BC,点D是AB的中点.

(1)求证:CD⊥平面A1ABB1;
(2)求证:AC1∥平面CDB1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com