
(本小题满分12分定义在R上的函数 满足
满足 ,当
,当 时,
时, .
.
(1)求 的值;
的值;
(2)比较 与
与 的大小.
的大小.
科目:高中数学 来源:2013届新疆喀什二中高二下期中文科数学(1、3、4部)(解析版) 题型:解答题
(本小题满分12分)
某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省豫南九校高三第四次联考文科数学 题型:解答题
(本小题满分12分)已知椭圆的中心在原点,焦点在 轴上,离心率为
轴上,离心率为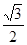 ,且经过点
,且经过点 ,直线
,直线 交椭圆于不同的两点A,B.(Ⅰ)求椭圆的方程;
交椭圆于不同的两点A,B.(Ⅰ)求椭圆的方程;
(Ⅱ)求 的取值范围;(Ⅲ)若直线
的取值范围;(Ⅲ)若直线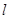 不过点M,试问
不过点M,试问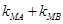 是否为定值?并说明理由。
是否为定值?并说明理由。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省高二上学期期末考试数学理卷 题型:解答题
(本小题满分12分)
已知直线 过抛物线
过抛物线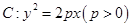 的焦点
的焦点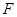 且与抛物线相交于两点
且与抛物线相交于两点 ,自
,自 向准线
向准线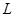 作垂线,垂足分别为
作垂线,垂足分别为 .
.
(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ)证明:无论 取何实数时,
取何实数时,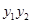 ,
, 都是定值;
都是定值;
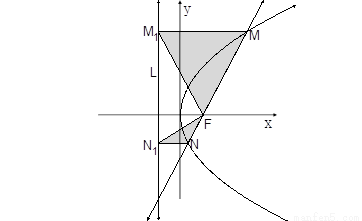 (III)记
(III)记 的面积分别为
的面积分别为 ,试判断
,试判断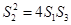 是否成立,并证明你的结论.
是否成立,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年海南省海口市高三高考调研考试理科数学 题型:解答题
((本小题满分12分)
如图,已知两定点 ,
,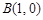 和定直线
和定直线 :
: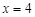 ,动点
,动点 在直线
在直线 上的射影为
上的射影为 ,且
,且 .
.
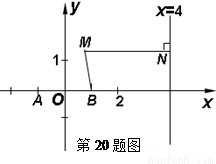
(Ⅰ)求动点 的轨迹
的轨迹 的方程并画草图;
的方程并画草图;
(Ⅱ)是否存在过点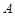 的直线
的直线 ,使得直线
,使得直线 与曲线
与曲线 相交于
相交于 ,
,  两点,且△
两点,且△ 的面积等于
的面积等于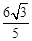 ?如果存在,请求出直线
?如果存在,请求出直线 的方程;如果不存在,请说明理由.
的方程;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省宜宾市高三第二次诊断性测试数学理卷 题型:解答题
((本小题满分12分)
已知点A(1,1)是椭圆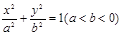 上一点,F1、F2是椭圆的两焦点,且满足|AF1|+|AF2|=4。
上一点,F1、F2是椭圆的两焦点,且满足|AF1|+|AF2|=4。
(I)求椭圆的标准方程;
(II)过点A(1,1)与椭圆相切的直线方程;
(III)设点C、D是椭圆上两点,直线AC、AD的倾斜角互补,试判断直线CD的斜率是否为定值?若是定值,求出定值;若不是定值,说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com