
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{2\sqrt{5}}{3}$ | C. | $\frac{\sqrt{10}}{2}$ | D. | $\frac{\sqrt{15}}{3}$ |
分析 利用在△PF1F2中,∠PF1F2的角平分线与另外两个角的外角平分线交于一点Q,Q点横坐标为4,可得|PF1|+|PF2|=8,利用$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=10,可得|PF1||PF2|cos∠PF1F2=10,由余弦定理可得20=|PF1|2+|PF2|2-2|PF1||PF2|cos∠PF1F2,可得|PF1|2+|PF2|2=40,||PF1|-|PF2||=4=2a,即可求出双曲线的离心率.
解答 解:设△PF1F2的旁切圆与PF1,PF2,F1F2,所在直线切于D,E,M,则DF1=MF1=4+c,MF2=EF2=4-c,PD=PE,
∴|PF1|+|PF2|=8,
∵$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=10,
∴|PF1||PF2|cos∠PF1F2=10,
由余弦定理可得20=|PF1|2+|PF2|2-2|PF1||PF2|cos∠PF1F2,
∴|PF1|2+|PF2|2=40,
∴|PF1||PF2|=12,
∴||PF1|-|PF2||=4=2a,
∴a=2,
∵c=$\sqrt{5}$,
∴e=$\frac{c}{a}$=$\frac{\sqrt{5}}{2}$.
故选:A.
点评 本题考查双曲线的离心率,考查余弦定理,考查学生分析解决问题的能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
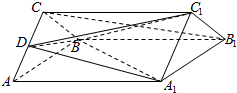 如图,在三棱柱ABC-A1B1C1中,棱AC的中点为D
如图,在三棱柱ABC-A1B1C1中,棱AC的中点为D查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 我国是世界上严重缺水的国家之一,城市缺水问题比较突处,某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,假设采用抽样调查方式,获得了100户居民某年的月均用水量(单位:t),并用这些样本数据分成9画出频率分布直方图,其中第3、4、5、6组的高度分别是0.15、0.22、0.25、0.14,第7、8、9、组高度比为3:2:1,直方图如图:
我国是世界上严重缺水的国家之一,城市缺水问题比较突处,某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,假设采用抽样调查方式,获得了100户居民某年的月均用水量(单位:t),并用这些样本数据分成9画出频率分布直方图,其中第3、4、5、6组的高度分别是0.15、0.22、0.25、0.14,第7、8、9、组高度比为3:2:1,直方图如图:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com