【题目】已知函数
的图象是由函数
的图象经如下变换得到：先将函数图象上所有点的横坐标缩短到原来的
倍（纵坐标不变），再将所得到的图象向左平移
个单位长度.
（1）写出函数的解析式和其图象的对称中心坐标.
（2）已知关于
的方程
在
上有两个不同的解
，
，求实数
的取值范围和
的值.
导学教程高中新课标系列答案科目：高中数学 来源： 题型：
【题目】孝感市旅游局为了了解双峰山景点在大众中的熟知度，从年龄在15～65岁的人群中随机抽取n人进行问卷调查，把这n人按年龄分成5组：第一组[15,25)，第二组[25,35)，第三组[35,45)，第四组[45,55)，第五组[55,65]，得到的样本的频率分布直方图如右：
调查问题是“双峰山国家森林公园是几A级旅游景点？”每组中回答正确的人数及回答正确的人数占本组的频率的统计结果如下表.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第1组 | [15,25) | 5 | 0.5 |
第2组 | [25,35) | 18 | x |
第3组 | [35,45) | y | 0.9 |
第4组 | [45,55) | 9 | a |
第5组 | [55,65] | 7 | b |
(1)分别求出n，x，y的值；
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人，求第2,3,4组每组各抽取多少人；
(3)在(2)抽取的6人中随机抽取2人，求所抽取的两人来自不同年龄组的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
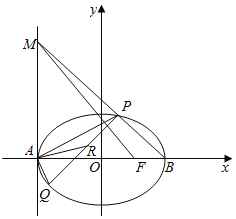
【题目】已知椭圆C：
的左右顶点为A、B，右焦点为F，一条准线方程是
，短轴一端点与两焦点构成等边三角形，点P、Q为椭圆C上异于A、B的两点，点R为PQ的中点
求椭圆C的标准方程；
直线PB交直线
于点M，记直线PA的斜率为
，直线FM的斜率为
，求证：
为定值；
若
，求直线AR的斜率的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校高三文科
名学生参加了
月份的高考模拟考试，学校为了了解高三文科学生的历史、地理学习情况，从名学生中抽取
名学生的成绩进行统计分析，抽出的名学生的地理、历史成绩如下表：
地理 历史 | [80,100] | [60,80） | [40,60） |
[80,100] | 8 | m | 9 |
[60,80） | 9 | n | 9 |
[40,60） | 8 | 15 | 7 |
若历史成绩在[80,100]区间的占30%，
（1）求
的值；
（2）请根据上面抽出的名学生地理、历史成绩，填写下面地理、历史成绩的频数分布表：
[80,100] | [60,80） | [40,60） | |
地理 | |||
历史 |
根据频数分布表中的数据估计历史和地理的平均成绩及方差（同一组数据用该组区间的中点值作代表），并估计哪个学科成绩更稳定.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角梯形
中，
，
，
，
，
，
为线段
（含端点）上的一个动点.设
，
，对于函数
，下列描述正确的是（ ）
A.
的最大值和
无关B.的最小值和无关
C.的值域和无关D.在其定义域上的单调性和无关
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知直线l过点A(-1,0)且与⊙B：
相切于点D，以坐标轴为对称轴的双曲线E过点D，一条渐近线平行于l，则E的离心率为（ ）
A. 
B. 2 C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】数学的对称美在中国传统文化中多有体现，譬如如图所示的太极图是由黑白两个鱼形纹组成的圆形图案，充分展现了相互转化、对称统一的和谐美.如果能够将圆的周长和面积同时平分的函数称为这个圆的“优美函数”，下列说法正确的是( )
A.对于任意一个圆，其“优美函数”有无数个
B.
可以是某个圆的“优美函数”
C.正弦函数
可以同时是无数个圆的“优美函数”
D.函数
是“优美函数”的充要条件为函数的图象是中心对称图形
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线C：x2=2py（p＞0）的焦点为F.过F的直线与抛物线C交于A、B，与抛物线C的准线交于M.
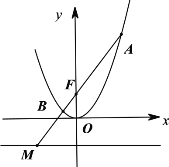
（1）若|AF|=|FM|=4，求常数p的值；
（2）设抛物线C在点A、B处的切线相交于N，求动点N的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
