
【题目】根据阅兵领导小组办公室介绍,2019年国庆70周年阅兵有59个方(梯)队和联合军乐团,总规模约1.5万人,是近几次阅兵中规模最大的一次.其中,徒步方队15个.为了保证阅兵式时队列保持整齐,各个方队对受阅队员的身高也有着非常严格的限制,太高或太矮都不行.徒步方队队员,男性身高普遍在175cm至185cm之间;女性身高普遍在163cm至175cm之间,这是常规标准.要求最为严格的三军仪仗队,其队员的身高一般都在184cm至190cm之间.经过随机调查某个阅兵阵营中女子100人,得到她们身高的直方图,如图,记C为事件:“某一阅兵女子身高不低于169cm”,根据直方图得到P(C)的估计值为0.5.

(1)求直方图中a,b的值;
(2)估计这个阵营女子身高的平均值 (同一组中的数据用该组区间的中点值为代表)
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】武汉出现的新型冠状病毒是一种可以通过飞沫传播的变异病毒,某药物研究所为筛查该新型冠状病毒,需要检验血液是否为阳性,现有![]() 份血液样本,每份样本取到的可能性均等,有以下两种检验方式:①逐份检验,则需要检验n次;②混合检验,将其中
份血液样本,每份样本取到的可能性均等,有以下两种检验方式:①逐份检验,则需要检验n次;②混合检验,将其中![]() 份血液样本分别取样混合在一起检验.若检验结果为阴性,这k份血液全为阴性,因此这k份血液样本检验一次就够了,如果检验结果为阳性,为了明确这k份血液究竟哪几份为阳性,就要对这k份血液再逐份检验,此时这k份血液的检验次数总共为
份血液样本分别取样混合在一起检验.若检验结果为阴性,这k份血液全为阴性,因此这k份血液样本检验一次就够了,如果检验结果为阳性,为了明确这k份血液究竟哪几份为阳性,就要对这k份血液再逐份检验,此时这k份血液的检验次数总共为![]() 次.假设在接受检验的血液样本中,每份样本的检验结果是阴性还是阳性都是独立的,且每份样本是阳性结果的概率为
次.假设在接受检验的血液样本中,每份样本的检验结果是阴性还是阳性都是独立的,且每份样本是阳性结果的概率为![]() .
.
(1)假设有5份血液样本,其中只有2份为阳性,若采取逐份检验方式,求恰好经过2次检验就能把阳性样本全部检验出来的概率;
(2)现取其中![]() 份血液样本,记采用逐份检验方式,样本需要检验的次数为
份血液样本,记采用逐份检验方式,样本需要检验的次数为![]() ,采用混合检验方式,样本需要检验的总次数为
,采用混合检验方式,样本需要检验的总次数为![]() .
.
(i)试运用概率统计知识,若![]() ,试求P关于k的函数关系式
,试求P关于k的函数关系式![]() ;
;
(ii)若![]() ,采用混合检验方式可以使得这k份血液样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求k的最大值.
,采用混合检验方式可以使得这k份血液样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求k的最大值.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在疫情这一特殊时期,教育行政部门部署了“停课不停学”的行动,全力帮助学生在线学习.复课后进行了摸底考试,某校数学教师为了调查高三学生这次摸底考试的数学成绩与在线学习数学时长之间的相关关系,对在校高三学生随机抽取45名进行调查.知道其中有25人每天在线学习数学的时长是不超过1小时的,得到了如下的等高条形图:
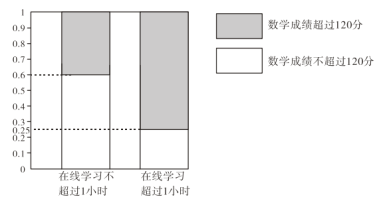
(Ⅰ)是否有![]() 的把握认为“高三学生的这次摸底考试数学成绩与其在线学习时长有关”;
的把握认为“高三学生的这次摸底考试数学成绩与其在线学习时长有关”;
(Ⅱ)将频率视为概率,从全校高三学生这次数学成绩超过120分的学生中随机抽取10人,求抽取的10人中每天在线学习时长超过1小时的人数的数学期望和方差.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
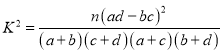
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】疫情过后,某商场开业一周累计生成2万张购物单,从中随机抽出100张,对每单消费金额进行统计得到下表:
消费金额(单位:元) |
|
|
|
|
|
购物单张数 | 25 | 25 | 30 | ? | ? |
由于工作人员失误,后两栏数据已无法辨识,但当时记录表明,根据由以上数据绘制成的频率分布直方图所估计出的每单消费额的中位数与平均数恰好相等(用频率估计概率),完成下列问题:
(1)估计该商场开业一周累计生成的购物单中,单笔消费额超过800元的购物单张数;
(2)为鼓励顾客消费,拉动内需,该商场打算在今年国庆期间进行促销活动,凡单笔消费超过600元者,可抽奖一次,中一等奖、二等奖、三等奖的顾客可以分别获得价值![]() 元、
元、![]() 元、
元、![]() 元的奖品.已知中奖率为100%,且一等奖、二等奖、三等奖的中奖率依次构成等差数列,其中一等奖的中奖率为
元的奖品.已知中奖率为100%,且一等奖、二等奖、三等奖的中奖率依次构成等差数列,其中一等奖的中奖率为![]() .若今年国庆期间该商场的购物单数量预计比疫情后开业一周的购物单数量增长5%,试预测商场今年国庆期间采办奖品的开销.
.若今年国庆期间该商场的购物单数量预计比疫情后开业一周的购物单数量增长5%,试预测商场今年国庆期间采办奖品的开销.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学举行了科学防疫知识竞赛.经过选拔,甲、乙、丙三位选手进入了最后角逐.他们还将进行四场知识竞赛.规定:每场知识竞赛前三名的得分依次为a,b,c(![]() ,且a,b,
,且a,b,![]() );选手总分为各场得分之和.四场比赛后,已知甲最后得分为16分,乙和丙最后得分都为8分,且乙只有一场比赛获得了第一名,则下列说法正确的是( )
);选手总分为各场得分之和.四场比赛后,已知甲最后得分为16分,乙和丙最后得分都为8分,且乙只有一场比赛获得了第一名,则下列说法正确的是( )
A.每场比赛的第一名得分a为4
B.甲至少有一场比赛获得第二名
C.乙在四场比赛中没有获得过第二名
D.丙至少有一场比赛获得第三名
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com