
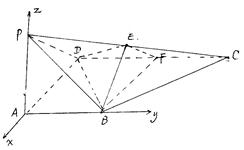
 , AB∥CD,AD=CD=2AB=2,E,F分别是PC,CD的中点.
, AB∥CD,AD=CD=2AB=2,E,F分别是PC,CD的中点. ,
,

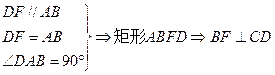 .………………………2分
.………………………2分
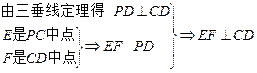 . ………………………………………5分
. ………………………………………5分 .…………………………………………8分
.…………………………………………8分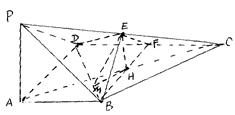 故
故 .
.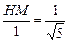 , 得
, 得 .
.
 得
得 ………………………………………………………12分
………………………………………………………12分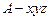 .
. ,
,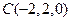 ,
,
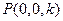 ,
, ,
, .………………………………………………………2分
.………………………………………………………2分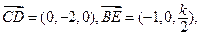
 .…………………………4分
.…………………………4分 ………………6分
………………6分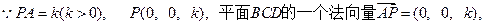 …7分
…7分  .
. ,
, 得
得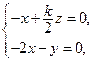 取
取 ……………10分 由
……………10分 由
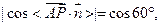 ………………………………………11分
………………………………………11分 …………………12分
…………………12分

 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源:不详 题型:解答题
 ,AC=3,BC=
,AC=3,BC= ,D是A1C的中点E是侧棱BB1上的一动点。
,D是A1C的中点E是侧棱BB1上的一动点。 的值
的值 的值,不存在则说明理由。
的值,不存在则说明理由。
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,设这条最短路线与CC1的交
,设这条最短路线与CC1的交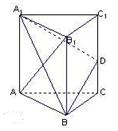
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
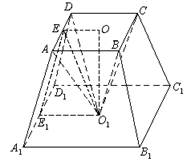
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
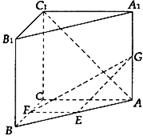
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com