
分析 设出弦的中点M,端点A,B的坐标,通过三点坐标的关系,把A,B的坐标代入椭圆方程后作差,代入直线l的斜率整理后即可得到答案;
解答 解:设斜率为2的弦中点M(x,y),A(x1,y1),B(x2,y2).
∵M为弦AB的中点,∴x1+x2=2x,y1+y2=2y.
则$\frac{{{x}_{1}}^{2}}{8}+\frac{{{y}_{1}}^{2}}{4}=1$,①
$\frac{{{x}_{2}}^{2}}{8}+\frac{{{y}_{2}}^{2}}{4}=1$,②
②-①得,$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$=-$\frac{1}{2}$×$\frac{{x}_{2}+{x}_{1}}{{y}_{2}+{y}_{1}}$.
∴$-\frac{x}{2y}=2$,整理得:x+4y=0.
由$\left\{\begin{array}{l}\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1\\ x+4y=0\end{array}\right.$,解得x=$±\frac{8}{3}$
所求轨迹方程为:x+y=0.(-$\frac{8}{3}$<x<$\frac{8}{3}$)
∴点P的轨迹方程为:x+4y=0(-$\frac{8}{3}$<x<$\frac{8}{3}$);
点评 本题考查了直线与圆锥曲线的关系,训练了“点差法”,涉及中点弦问题.利用点差法能起到事半功倍的作用,该题是中档题.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{x}$ | B. | x | C. | $\frac{x-1}{x+1}$ | D. | $\frac{1+x}{1-x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
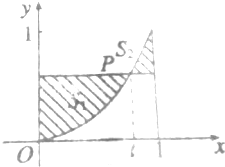 如图,在曲线C:y=x2,x∈[0,1]上取点P(t,t2),过点P作x轴的平行线l,曲线C于直线x=0,x=1及直线l围成的图形面积分别记为S1、S2.
如图,在曲线C:y=x2,x∈[0,1]上取点P(t,t2),过点P作x轴的平行线l,曲线C于直线x=0,x=1及直线l围成的图形面积分别记为S1、S2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com