
【题目】已知△ABC的角A,B,C所对的边分别为a,b,c,且 ![]() . (Ⅰ)求角A的大小;
. (Ⅰ)求角A的大小;
(Ⅱ)若a=1, ![]() ,求b+c的值.
,求b+c的值.
【答案】解:(Ⅰ)△ABC中,∵ ![]() , ∴sinAcosB+
, ∴sinAcosB+ ![]() sinBsinA=sinC,
sinBsinA=sinC,
∵sinC=sin(A+B)=sinAcosB+cosAsinB
∴sinAcosB+ ![]() sinBsinA=sinAcosB+cosAsinB
sinBsinA=sinAcosB+cosAsinB
整理得 ![]() sinA=cosA,即tanA=
sinA=cosA,即tanA= ![]() ,
,
∴A= ![]() .
.
(Ⅱ)ABACcosA=| ![]()
![]() |=3,
|=3,
∴bc ![]() =3,即bc=2
=3,即bc=2 ![]() ,
,
∵a2=b2+c2﹣2bccosA,即1=b2+c2﹣22 ![]()
![]() ,
,
∴b2+c2=1+6=7,
∴b+c= ![]() =
= ![]()
【解析】(Ⅰ)利用正弦定理把已知等式转化成角的正弦的关系式,整理求得tanA的值,进而求得A.(Ⅱ)利用向量积的性质求得bc的值,进而利用余弦定理求得b2+c2的值,最后用配方法求得答案.
【考点精析】掌握正弦定理的定义是解答本题的根本,需要知道正弦定理:![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上. (Ⅰ)求异面直线D1E与A1D所成的角;
(Ⅱ)若二面角D1﹣EC﹣D的大小为45°,求点B到平面D1EC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点P与两定点A(﹣2,0),B(2,0)连线的斜率之积为﹣ ![]() . (Ⅰ)求动点P的轨迹C的方程;
. (Ⅰ)求动点P的轨迹C的方程;
(Ⅱ)若过点F(﹣ ![]() ,0)的直线l与轨迹C交于M、N两点,且轨迹C上存在点E使得四边形OMEN(O为坐标原点)为平行四边形,求直线l的方程.
,0)的直线l与轨迹C交于M、N两点,且轨迹C上存在点E使得四边形OMEN(O为坐标原点)为平行四边形,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f0(x)=sinx,f1(x)=f0′(x),f2(x)=f1′(x),…,fn+1(x)=fn′(x),n∈N,则f2006(x)=( )
A.sinx
B.﹣sinx
C.cosx
D.﹣cosx
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市电视台为了宣传,举办问答活动,随机对该市15至65岁的人群进行抽样,频率分布直方图及回答问题统计结果如表所示:
组号 | 分组 | 回答正确 | 回答正确的人数 |
第1组 | [15,25) | 5 | 0.5 |
第2组 | [25,35) | a | 0.9 |
第3组 | [35,45) | 27 | x |
第4组 | [45,55) | b | 0.36 |
第5组 | [55,65) | 3 | y |
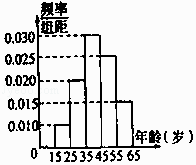
(1)分别求出a,b,x,y的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,电视台决定在所抽取的6人中随机抽取3人颁发幸运奖,求:所抽取的人中第3组至少有1人获得幸运奖的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com