
【题目】已知数列![]() 是等比数列,有下列四个命题:①
是等比数列,有下列四个命题:①![]() 是等比数列;②
是等比数列;②![]() 是等比数列;③
是等比数列;③![]() 是等比数列;④
是等比数列;④![]() 是等比数列,其中正确命题的序号是( )
是等比数列,其中正确命题的序号是( )
A.②④B.③④C.②③④D.①②③④
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】居民消费价格指数(Consumer Price Index,简称![]() ),是度量居民生活消费品和服务价格水平随着时间变动的相对数,综合反映居民购买的生活消费品和服务价格水平的变动情况.如图为国家统计局于2020年4月公布的2019年3月至2020年3月
),是度量居民生活消费品和服务价格水平随着时间变动的相对数,综合反映居民购买的生活消费品和服务价格水平的变动情况.如图为国家统计局于2020年4月公布的2019年3月至2020年3月![]() 数据同比和环比涨跌幅折线图:
数据同比和环比涨跌幅折线图:
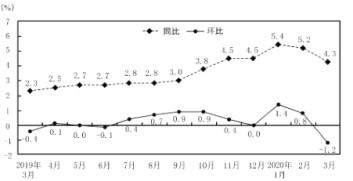
(注:同比![]() ,同比涨跌幅
,同比涨跌幅![]() ,环比
,环比![]() ,环比涨跌幅
,环比涨跌幅![]() ),则下列说法正确的是( )
),则下列说法正确的是( )
A.2019年12月与2018年12月![]() 相等
相等
B.2020年3月比2019年3月![]() 上涨4.3%
上涨4.3%
C.2019年7月至2019年11月![]() 持续增长
持续增长
D.2020年1月至2020年3月![]() 持续下降
持续下降
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() 是边长为2的正三角形,已知
是边长为2的正三角形,已知![]() 点满足
点满足![]() .
.
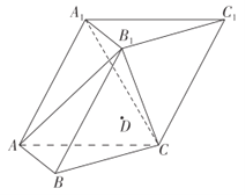
(1)求二面角![]() 的大小;
的大小;
(2)求异面直线![]() 与
与![]() 的距离;
的距离;
(3)直线![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面?若存在,请确定点
平面?若存在,请确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .以极点为原点,极轴为
.以极点为原点,极轴为![]() 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)若![]() ,求曲线
,求曲线![]() 的直角坐标方程以及直线
的直角坐标方程以及直线![]() 的极坐标方程;
的极坐标方程;
(2)设点![]() ,曲线
,曲线![]() 与直线
与直线![]() 交于两点,求
交于两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.命题“![]() ”的否定是“
”的否定是“![]() ”
”
B.命题“已知![]() ,若
,若![]() 则
则![]() 或
或![]() ”是真命题
”是真命题
C.命题“若![]() 则函数
则函数![]() 只有一个零点”的逆命题为真命题
只有一个零点”的逆命题为真命题
D.“![]() 在
在![]() 上恒成立”
上恒成立”![]() 在
在![]() 上恒成立
上恒成立
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和为Sn,若对任意正整数n,总存在正整数m,使得Sn=am,则称数列{an}为S数列.
(1)S数列的任意一项是否可以写成其某两项的差?请说明理由.
(2)①是否存在等差数列为S数列,若存在,请举例说明;若不存在,请说明理由.
②是否存在正项递增等比数列为S数列,若存在,请举例说明;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com