Question

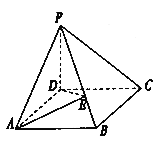
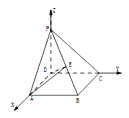
【题目】如图在棱锥中， 为矩形， 面， ， 与面成角， 与面成角.

（1）在上是否存在一点，使面，若存在确定点位置，若不存在，请说明理由；

（2）当为中点时，求二面角的余弦值.

Answer 1

【答案】（1）见解析（2）

【解析】试题分析：（1）法一：要证明PC⊥面ADE，只需证明AD⊥PC，通过证明即可，然后推出存在点E为PC中点．

法二：建立如图所示的空间直角坐标系D﹣XYZ，设，通过得到，即存在点E为PC中点．

（2）由（1）知求出面ADE的法向量，面PAE的法向量，利用空间向量的数量积．求解二面角P﹣AE﹣D的余弦值．

试题解析：

（Ⅰ）法一：要证明PC⊥面ADE，易知AD⊥面PDC，即得AD⊥PC，故只需即可，所以由,即存在点E为PC中点

法二：建立如图所示的空间直角坐标系D－XYZ，

由题意知PD＝CD＝1，

，设， ，

,

由，得，

即存在点E为PC中点。

（Ⅱ）由（Ⅰ）知， ， ，

， ， ，

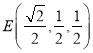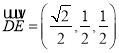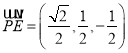
设面ADE的法向量为，面PAE的法向量为

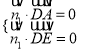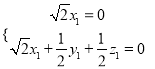由的法向量为得， 得

同理求得 所以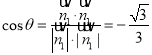

故所求二面角P－AE－D的余弦值为.