
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图,观察图形的信息,回答下列问题:

(1)求分数在[120,130)内的频率;
(2)估计本次考试的中位数;
(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人在分数段[120,130)内的概率.
【答案】(1)0.3;(2)![]() (3)
(3)![]()
【解析】
(1)根据频率分布直方图的各小长方形的面积之和为1,求出分数在![]() 内的概率;(2)由直方图左右两边面积相等处横坐标计算出中位数;(3)计算出
内的概率;(2)由直方图左右两边面积相等处横坐标计算出中位数;(3)计算出![]() 与
与![]() 分数段的人数,用分层抽样的方法求出在各分数段内抽取的人数组成样本,利用古典概率公式求出“从样本中任取2人,至多有1人在分数段
分数段的人数,用分层抽样的方法求出在各分数段内抽取的人数组成样本,利用古典概率公式求出“从样本中任取2人,至多有1人在分数段![]() 内”的概率即可.
内”的概率即可.
(1)分数在[120,130)内的频率为
1﹣(0.1+0.15+0.15+0.25+0.05)=1﹣0.7=0.3;
(2)由于图中前3个小矩形面积之和为0.4
则设中位数![]() ,则
,则
![]() ,则
,则![]()
(3)依题意,[110,120)分数段的人数为60×0.15=9(人),
[120,130)分数段的人数为60×0.3=18(人);
∵用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,
∴需在[110,120)分数段内抽取2人,并分别记为m,n;
在[120,130)分数段内抽取4人,并分别记为a,b,c,d;
设“从样本中任取2人,至多有1人在分数段[120,130)内”为事件A,
则基本事件有(m,n),(m,a),…,(m,d),(n,a),…,(n,d),(a,b),…,(c,d)共15种;
则事件A包含的基本事件有(m,n),(m,a),(m,b),(m,c),(m,d),(n,a),(n,b),(n,c),(n,d)共9种;∴P(A)=![]() =
=![]()


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
【题目】(题文)(12分)设f(x)=2x3+ax2+bx+1的导数为f′(x),若函数y=f′(x)的图象关于直线x=﹣![]() 对称,且f′(1)=0
对称,且f′(1)=0
(Ⅰ)求实数a,b的值
(Ⅱ)求函数f(x)的极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cosx+sinx,2sinx),
=(cosx+sinx,2sinx), ![]() =(cosx﹣sinx,cosx).令f(x)=
=(cosx﹣sinx,cosx).令f(x)= ![]()
![]() .
.
(1)求f(x)的最小正周期;
(2)求f(x)在[ ![]() ,
, ![]() ]上的单调递增区间.
]上的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.

(Ⅰ)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(Ⅱ)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据:![]() ,
,![]() ,
,
![]() ,
,![]() ≈2.646.
≈2.646.
参考公式:相关系数
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,已知点A(a,a),B(2,3),C(3,2).
(1)若向量 ![]() ,
, ![]() 的夹角为钝角,求实数a的取值范围;
的夹角为钝角,求实数a的取值范围;
(2)若a=1,点P(x,y)在△ABC三边围成的区域(含边界)上, ![]() =m
=m ![]() +n
+n ![]() (m,n∈R),求m﹣n的最大值.
(m,n∈R),求m﹣n的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读如图所示的程序框图,则该算法的功能是( ) 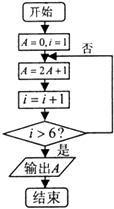
A.计算数列{2n﹣1}前5项的和
B.计算数列{2n﹣1}前5项的和
C.计算数列{2n﹣1}前6项的和
D.计算数列{2n﹣1}前6项的和
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sinxcosx+2 ![]() cos2x﹣
cos2x﹣ ![]()
(1)求函数f(x)的最小正周期和单调减区间;
(2)已知△ABC的三个内角A,B,C的对边分别为a,b,c,其中a=7,若锐角A满足f( ![]() ﹣
﹣ ![]() )=
)= ![]() ,且sinB+sinC=
,且sinB+sinC= ![]() ,求bc的值.
,求bc的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两点M(﹣3,0),N(3,0),点P为坐标平面内一动点,且![]() ,则动点P(x,y)到两点A(﹣3,0)、B(﹣2,3)的距离之和的最小值为( )
,则动点P(x,y)到两点A(﹣3,0)、B(﹣2,3)的距离之和的最小值为( )
A. 4 B. 5 C. 6 D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com