
【题目】已知椭圆方程![]() ,其左焦点、上顶点和左顶点分别为
,其左焦点、上顶点和左顶点分别为![]() ,
, ![]() ,
, ![]() ,坐标原点为
,坐标原点为![]() ,且线段
,且线段![]() ,
, ![]() ,
, ![]() 的长度成等差数列.
的长度成等差数列.
(Ⅰ)求椭圆的离心率;
(Ⅱ)若过点![]() 的一条直线
的一条直线![]() 交椭圆于点
交椭圆于点![]() ,
, ![]() ,交
,交![]() 轴于点
轴于点![]() ,使得线段
,使得线段![]() 被点
被点![]() ,
, ![]() 三等分,求直线
三等分,求直线![]() 的斜率.
的斜率.
 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 是圆
是圆![]() 上任意一点,点
上任意一点,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 分别与线段
分别与线段![]() 交于
交于![]() 两点,且
两点,且![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)直线![]() 与轨迹
与轨迹![]() 相交于
相交于![]() 两点,设
两点,设![]() 为坐标原点,
为坐标原点, ![]() ,判断
,判断![]() 的面积是否为定值?若是,求出定值,若不是,说明理由.
的面积是否为定值?若是,求出定值,若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下关于命题的说法正确的有(选择所有正确命题的序号).
(1)“若![]() ,则函数
,则函数![]() 在其定义域内是减函数”是真命题;
在其定义域内是减函数”是真命题;
(2)命题“若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”;
”;
(3)命题“若![]() 都是偶函数,则
都是偶函数,则![]() 也是偶数”的逆命题为真命题;
也是偶数”的逆命题为真命题;
(4)命题“若![]() ,则
,则![]() ”与命题“若
”与命题“若![]() ,则
,则![]() ”等价.
”等价.
A. (1)(3) B. (2)(3) C. (2)(4) D. (3)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 上的点到两个焦点的距离之和为
上的点到两个焦点的距离之和为![]() ,短轴长为
,短轴长为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 相切,探究
相切,探究![]() 是否为定值,如果是定值,请求出该定值;如果不是定值,请说明理由.
是否为定值,如果是定值,请求出该定值;如果不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现如今,“网购”一词不再新鲜,越来越多的人已经接受并喜欢了这种购物方式,但随之也出现了商品质量不能保证与信誉不好等问题,因此,相关管理部门制定了针对商品质量与服务的评价体系,现从评价系统中选出成功交易200例,并对其评价进行统计:对商品的好评率为0.6,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为80次.
(1)依据题中的数据完成下表,并通过计算说明,能否有99.9%的把握认为“商品好评与服务好评”有关;
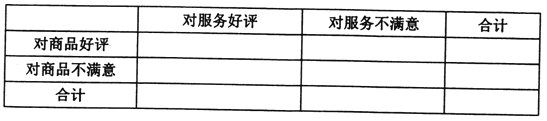
(2)若将频率视为概率,某人在该购物平台上进行了5次购物,设对商品和服务全好评的次数为随机变量![]() ,求
,求![]() 的分布列(概率用算式表示)、数学期望和方差.
的分布列(概率用算式表示)、数学期望和方差.

查看答案和解析>>
科目:高中数学 来源: 题型:
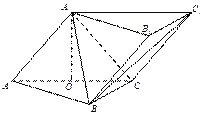
【题目】如下图,三棱柱![]() 中,侧面
中,侧面![]()
![]() 底面
底面![]() ,
, ![]() ,且
,且![]() ,O为
,O为![]() 中点.
中点.
(Ⅰ)证明: ![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦;
所成角的正弦;
(Ⅲ)在![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,若不存在,说明理由;若存在,确定点
,若不存在,说明理由;若存在,确定点![]() 的位置.
的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点. 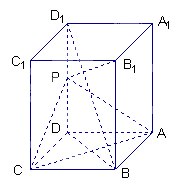
(1)求证:直线BD1∥平面PAC;
(2)求证:直线PB1⊥平面PAC.
(3)求三棱锥B﹣PAC的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com