
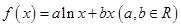 在点
在点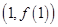 处的切线方程为
处的切线方程为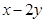
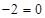 .
.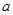 、
、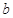 的值;
的值; 时,
时,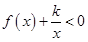 恒成立,求实数
恒成立,求实数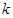 的取值范围;
的取值范围;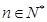 ,且
,且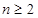 时,
时,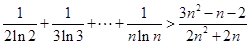 .
.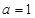 ,
,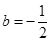 ;(2)
;(2)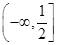 ;(3)详见解析.
;(3)详见解析.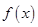 在
在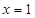 处的导数值
处的导数值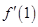 ,二是切点在切线上也在函数
,二是切点在切线上也在函数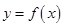 的图象上,通过切点
的图象上,通过切点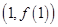 在切线上求出
在切线上求出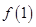 的值,然后再通过
的值,然后再通过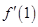 和
和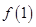 的值列有关
的值列有关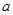 、
、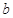 的二元一次方程组,求出
的二元一次方程组,求出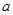 、
、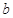 的值;(2)解法1是利用参数分离法将不等式
的值;(2)解法1是利用参数分离法将不等式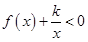 在区间
在区间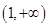 上恒成立问题转化为不等式
上恒成立问题转化为不等式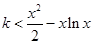 在区间
在区间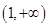 上恒成立,并构造函数
上恒成立,并构造函数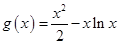 ,从而转化为
,从而转化为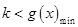 ,并利用导数求出函数
,并利用导数求出函数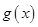 的最小值,从而求出
的最小值,从而求出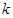 的取值范围;解法2是构造新函数
的取值范围;解法2是构造新函数 ,将不等式
,将不等式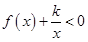 在区间
在区间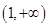 上恒成立问题转化为不等式
上恒成立问题转化为不等式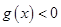 在区间
在区间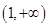 上恒成立问题,等价于
上恒成立问题,等价于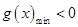 利用导数研究函数
利用导数研究函数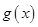 的单调性,对
的单调性,对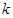 的取值进行分类讨论,通过在不同取值条件下确定函数
的取值进行分类讨论,通过在不同取值条件下确定函数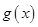 的单调性求出
的单调性求出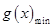 ,围绕
,围绕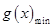
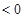 列不等式求解,从而求出
列不等式求解,从而求出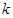 的取值范围;(3)在(2)的条件下得到
的取值范围;(3)在(2)的条件下得到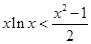 ,在不等式两边为正数的条件下两边取倒数得到
,在不等式两边为正数的条件下两边取倒数得到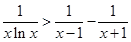 ,然后分别令
,然后分别令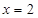 、
、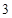 、
、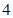 、
、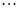 、
、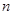 ,利用累加法以及同向不等式的相加性来证明问题中涉及的不等式.
,利用累加法以及同向不等式的相加性来证明问题中涉及的不等式. ,
, .
. 直线
直线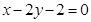 的斜率为
的斜率为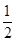 ,且过点
,且过点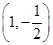 ,
, ,即
,即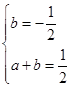 解得
解得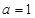 ,
,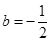 ;
; .
. 时,
时,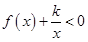 恒成立,即
恒成立,即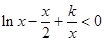 ,等价于
,等价于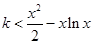 .
.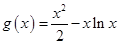 ,则
,则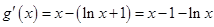 .
.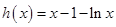 ,则
,则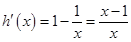 .
. 时,
时,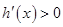 ,函数
,函数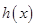 在
在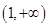 上单调递增,故
上单调递增,故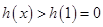 .
. 时,
时,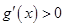 ,即函数
,即函数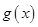 在
在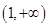 上单调递增,
上单调递增,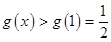 .
. 时,
时,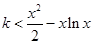 恒成立,则
恒成立,则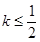 .
. 所求
所求 的取值范围是
的取值范围是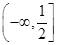 ;
; .
. 时,
时,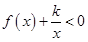 恒成立,即
恒成立,即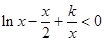 恒成立.
恒成立. ,则
,则 .
. (*)的判别式
(*)的判别式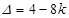 .
.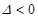 ,即
,即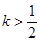 时,则
时,则 时,
时,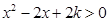 ,得
,得 ,
,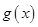 在
在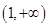 上单调递减.
上单调递减.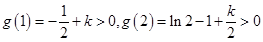 ,
,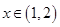 时,
时,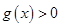 ,即
,即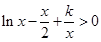 ,与题设矛盾;
,与题设矛盾;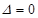 ,即
,即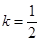 时,则
时,则 时,
时, .
.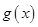 在
在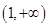 上单调递减,则
上单调递减,则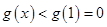 ,符合题意;
,符合题意;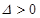 ,即
,即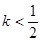 时,方程(*)的两根为
时,方程(*)的两根为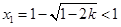 ,
,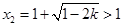 ,
,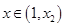 时,
时,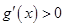 ,
,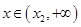 时,
时, .
.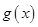 在
在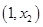 上单调递增,在
上单调递增,在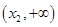 上单调递减,
上单调递减,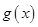 在
在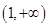 上的最大值为
上的最大值为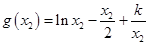 .
.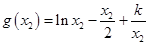
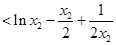 ,
, 时,
时, ,
,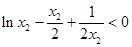 ,从而
,从而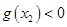 .
. 时,
时,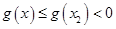 ,符合题意.
,符合题意.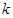 的取值范围是
的取值范围是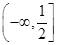 .
. 时,
时, ,可化为
,可化为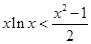 ,
,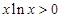 ,从而,
,从而,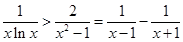 .
.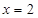 、
、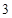 、
、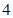 、
、 、
、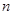 分别代入上面不等式,并相加得,
分别代入上面不等式,并相加得,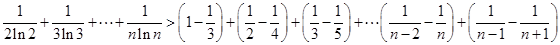
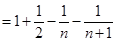
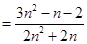 .
.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源:不详 题型:解答题
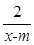 在区间(1,+∞)上是减函数;命题q:x1,x2是方程x2-ax-2=0的两个实根,且不等式m2+5m-3≥|x1-x2|对任意的实数a∈[-1,1]恒成立.若
在区间(1,+∞)上是减函数;命题q:x1,x2是方程x2-ax-2=0的两个实根,且不等式m2+5m-3≥|x1-x2|对任意的实数a∈[-1,1]恒成立.若 p∧q为真,试求实数m的取值范围.
p∧q为真,试求实数m的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com