
如图,四边形ABCD中,AB=AD=CD=1,BD=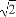 ,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A'-BCD,使平面A'BD⊥平面BCD,则下列结论正确的是( )
,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A'-BCD,使平面A'BD⊥平面BCD,则下列结论正确的是( )

(A)A'C⊥BD
(B)∠BA'C=90°
(C)CA'与平面A'BD所成的角为30°
(D)四面体A'-BCD的体积为
B
【解析】折叠前AB=AD=1,BD=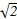 ,即AB⊥AD,折叠后平面A'BD⊥平面BCD,且CD⊥BD,故CD⊥平面A'BD.
,即AB⊥AD,折叠后平面A'BD⊥平面BCD,且CD⊥BD,故CD⊥平面A'BD.
取BD的中点O,∵A'B=A'D,
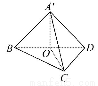
∴A'O⊥BD.又平面A'BD⊥平面BCD,平面A'BD∩平面BCD=BD,
∴A'O⊥平面BCD.
∵CD⊥BD,
∴OC不垂直于BD.假设A'C⊥BD,
∵OC为A'C在平面BCD内的射影,
∴OC⊥BD,矛盾,∴A'C不垂直于BD,A错误;
∵CD⊥BD,平面A'BD⊥平面BCD,
∴CD⊥平面A'BD,A'C在平面A'BD内的射影为A'D.
∵A'B=A'D=1,BD=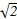 ,
,
∴A'B⊥A'D,A'B⊥A'C,B正确;∠CA'D为直线CA'与平面A'BD所成的角,
∠CA'D=45°,C错误;
VA'-BCD=VC-A'BD=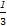 S△A'BD·CD=
S△A'BD·CD=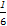 ,D错误.
,D错误.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(三)第一章第三节练习卷(解析版) 题型:填空题
已知条件p:x2-x≥6;q:x∈Z,当x∈M时,“p且q”与“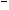 q”同时为假命题,则x取值组成的集合M= .
q”同时为假命题,则x取值组成的集合M= .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(一)第一章第一节练习卷(解析版) 题型:选择题
A={x|x≠1,x∈R}∪{y|y≠2,y∈R},B={z|z≠1且z≠2,z∈R},那么( )
(A)A=B (B)A B
B
(C)B A (D)A∩B=?
A (D)A∩B=?
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十四第七章第三节练习卷(解析版) 题型:选择题
如图是某个正方体的侧面展开图,l1,l2是两条侧面对角线,则在正方体中,l1与l2( )
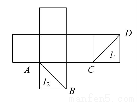
(A)互相平行
(B)异面且互相垂直
(C)异面且夹角为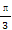
(D)相交且夹角为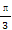
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十六第七章第五节练习卷(解析版) 题型:解答题
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=∠CAD=90°,且PA=AB=BC,点E是棱PB上的动点.
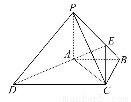
(1)若PD∥平面EAC,试确定点E在棱PB上的位置.
(2)在(1)的条件下,求二面角A-CE-P的余弦值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十六第七章第五节练习卷(解析版) 题型:选择题
设l,m,n为三条不同的直线,α,β为两个不同的平面,下列命题中正确的个数是( )
①若l⊥α,m∥β,α⊥β,则l⊥m;
②若m?α,n?α,l⊥m,l⊥n,则l⊥α;
③若l∥m,m∥n,l⊥α,则n⊥α;
④若l∥m,m⊥α,n⊥β,α∥β,则l∥n.
(A)1 (B)2 (C)3 (D)4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十八第七章第七节练习卷(解析版) 题型:填空题
已知l∥α,且l的方向向量为u=(2,m,1),平面α的法向量为v=(1, ,2),则m= .
,2),则m= .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十五第七章第四节练习卷(解析版) 题型:选择题
如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A'DE是△ADE绕DE旋转过程中的一个图形(A'不与A,F重合),则下列命题中正确的是( )
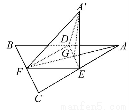
①动点A'在平面ABC上的射影在线段AF上;
②BC∥平面A'DE;③三棱锥A'-FED的体积有最大值.
(A)① (B)①② (C)①②③ (D)②③
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十三第七章第二节练习卷(解析版) 题型:解答题
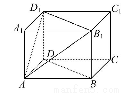
如图,在长方体ABCD-A1B1C1D1中,AB=AD=3cm,AA1=2cm,则四棱锥A-BB1D1D的体积为 cm3.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com