
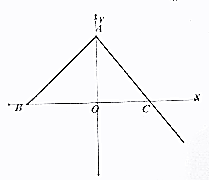
 已知在平面直角坐标系中,O为坐标原点,A(0,4)、B(-4,0),点C是x轴正半轴上的点,△ABC的面积是14,O到AC的距离是$\frac{12}{5}$,动点P从A出发以每秒3个单位长度的速度沿射线AC运动,同时动点Q从C点出发以每秒2个单位的速度沿x轴的正方向运动.
已知在平面直角坐标系中,O为坐标原点,A(0,4)、B(-4,0),点C是x轴正半轴上的点,△ABC的面积是14,O到AC的距离是$\frac{12}{5}$,动点P从A出发以每秒3个单位长度的速度沿射线AC运动,同时动点Q从C点出发以每秒2个单位的速度沿x轴的正方向运动.分析 (1)通过设C(x,0),其中x>0,利用S△ABC=$\frac{1}{2}$|OA|•|BC|=14计算即得结论;
(2)通过(1)可知|AC|=5,通过当BP⊥AC时S△ABC=$\frac{1}{2}$|AC|•|BP|计算可知|BP|=$\frac{28}{5}$,利用勾股定理可知|AP|=$\frac{4}{5}$,利用$\frac{|AP|}{|AH|}$=cos∠OAC=$\frac{|OA|}{|AC|}$计算可知|AH|=1;
(3)通过当△CPQ是以PQ为底边的等腰三角形时|CP|=|CQ|,代入计算即得结论.
解答  解:(1)设C(x,0),其中x>0,
解:(1)设C(x,0),其中x>0,
则S△ABC=$\frac{1}{2}$|OA|•|BC|=$\frac{1}{2}$×4×[x-(-4)]=2x+8=14,
解得:x=3,
故点C的坐标为(3,0);
(2)由(1)可知|AC|=$\sqrt{{3}^{2}+{4}^{2}}$=5,
当BP⊥AC时,S△ABC=$\frac{1}{2}$|AC|•|BP|,
即14=$\frac{1}{2}×5×$|BP|,解得:|BP|=$\frac{28}{5}$,
∴|AP|=$\sqrt{|AB{|}^{2}-|BP{|}^{2}}$=$\sqrt{|OB{|}^{2}+|OA{|}^{2}-|BP{|}^{2}}$=$\sqrt{{4}^{2}+{4}^{2}-(\frac{28}{5})^{2}}$=$\frac{4}{5}$,
又∵$\frac{|AP|}{|AH|}$=cos∠HAP=cos∠OAC=$\frac{|OA|}{|AC|}$,即$\frac{\frac{4}{5}}{|AH|}$=$\frac{4}{5}$,
∴|AH|=1,
故AH的长为1;
(3)依题意,当△CPQ是以PQ为底边的等腰三角形时,
有|CP|=|CQ|,即3t-|AC|=2t,
∴3t-5=2t,解得:t=5,
故当t=5时△CPQ是以PQ为底边的等腰三角形.
点评 本题考查根据实际问题选择函数类型,考查数列结合能力,注意解题方法的积累,属于中档题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | -1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2-2x+1≤0 | B. | x2-2x+1≥0 | C. | x2-2x+1>0 | D. | x2-2x+1<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com