
【题目】我国上是世界严重缺水的国家,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准![]() (吨),用水量不超过
(吨),用水量不超过![]() 的部分按平价收费,超过
的部分按平价收费,超过![]() 的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照
的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照![]() ,
, ![]() ,…,
,…, ![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
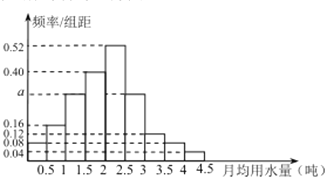
(Ⅰ)求直方图中![]() 的值;
的值;
(Ⅱ)已知该市有80万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)若该市政府希望使![]() 的居民每月的用水量不超过标准
的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值,并说明理由;
的值,并说明理由;
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ) ![]() 人 ;(Ⅲ) 估计月用水量标准为2.9吨时,85%的居民每月的用水量不超过标准.
人 ;(Ⅲ) 估计月用水量标准为2.9吨时,85%的居民每月的用水量不超过标准.
【解析】试题分析:(Ⅰ)利用频率分布直方图中的矩形面积的和为1求![]() 的值;(Ⅱ)首先计算月均用水量大于等于3吨的频率,80万乘以频率就是所求的人数;(Ⅲ)首先大体估计
的值;(Ⅱ)首先计算月均用水量大于等于3吨的频率,80万乘以频率就是所求的人数;(Ⅲ)首先大体估计![]() 的区间,再计算区间
的区间,再计算区间![]() 的频率和为0.85时,求解
的频率和为0.85时,求解![]() 的值.
的值.
试题解析:(Ⅰ)由频率分布直方图,可得
![]() ,
,
解得![]() .
.
(Ⅱ)由频率分布直方图可知,100位居民每人月用水量不低于3吨的人数为
![]() ,
,
由以上样本频率分布,可以估计全市80万居民中月均用水量不低于3吨的人数为
![]() .
.
(Ⅲ) ![]() 前6组的频率之和为
前6组的频率之和为![]() ,
,
而前5组的频率之和为![]() ,
,
![]()
由![]() ,解得
,解得![]() ,
,
因此,估计月用水量标准为2.9吨时,85%的居民每月的用水量不超过标准.


 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:高中数学 来源: 题型:
【题目】若函数f(x)对任意的x∈R都有f′(x)>f(x)恒成立,则( )
A.3f(ln2)>2f(ln3)
B.3f(ln2)=2f(ln3)
C.3f(ln2)<2f(ln3)
D.3f(ln2)与2f(ln3)的大小不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线![]() ,曲线
,曲线![]() .以极点为坐标原点,极轴为
.以极点为坐标原点,极轴为![]() 轴正半轴建立平面直角坐标系
轴正半轴建立平面直角坐标系![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为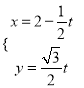 (
(![]() 为参数).
为参数).
(1)求![]() 的直角坐标方程;
的直角坐标方程;
(2)![]() 与
与![]() 交于不同的四点,这四点在
交于不同的四点,这四点在![]() 上排列顺次为
上排列顺次为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数fn(x)=xn+bx+c(n∈N* , b,c∈R)
(Ⅰ)设n≥2,b=1,c=﹣1,证明:fn(x)在区间( ![]() )内存在唯一的零点;
)内存在唯一的零点;
(Ⅱ)设n=2,若对任意x1 , x2∈[﹣1,1],均有|f2(x1)﹣f2(x2)丨≤4,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在![]() △
△![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 分别为边
分别为边![]() 的中点,点
的中点,点![]() 分别为线段
分别为线段![]() 的中点.将△
的中点.将△![]() 沿
沿![]() 折起到△
折起到△![]() 的位置,使
的位置,使![]() .点
.点![]() 为线段
为线段![]() 上的一点,如图2.
上的一点,如图2.
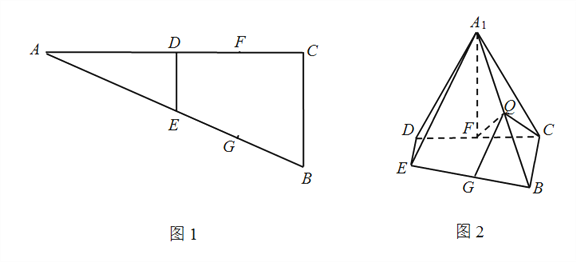
(Ⅰ)求证: ![]() ;
;
(Ⅱ)线段![]() 上是否存在点
上是否存在点![]() 使得
使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的长,若不存在,请说明理由;
的长,若不存在,请说明理由;
(Ⅲ)当![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:方程 ![]() =1所表示的图形是焦点在y轴上的双曲线,命题q:复数z=(m﹣3)+(m﹣1)i对应的点在第二象限,又p或q为真,p且q为假,求实数m的取值范围.
=1所表示的图形是焦点在y轴上的双曲线,命题q:复数z=(m﹣3)+(m﹣1)i对应的点在第二象限,又p或q为真,p且q为假,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中正确的序号是 .
①函数y=ax(a>0且a≠1)与函数 ![]() (a>0且a≠1)的定义域相同;
(a>0且a≠1)的定义域相同;
②函数y=k3x(k>0)(k为常数)的图象可由函数y=3x的图象经过平移得到;
③函数 ![]() (x≠0)是奇函数且函数
(x≠0)是奇函数且函数 ![]() (x≠0)是偶函数;
(x≠0)是偶函数;
④若x1是函数f(x)的零点,且m<x1<n,则f(m)f(n)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖,若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为X,求X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com