练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某学校有初级教师21人，中级教师14人，高级教师7人，现采用分层抽样的方法从这些教师中抽取6人对绩效工资情况进行调查．

    (1)求应从初级教师，中级教师，高级教师中分别抽取的人数；

    (2)若从抽取的6名教师中随机抽取2名做进一步数据分析，求抽取的2名均为初级教师的概率。

    【答案】（1）3,2,1； （2）.

    【解析】

    (1)先求出每位教师被抽到的概率，再用每层的教师数乘以毎位教师被柚到的概率，即得应从每层教师中抽取的人数；(2) 从初级教师、中级教师、高级教师中分别抽取的人数为3,2,1，列出抽取2名教师的所有可能结果，以及从6名教师中抽取的2名教师均为初级教师的结果，利用古典概型的概率公式计算，即可得到结果.

    （1）从初级教师、中级教师、高级教师中分别抽取的人数为3,2,1.

    ( 2 )在抽取到的6名教师中，3名初级教师分别记为A1，A2，A3,2名中级教师分别记为A4，A5，高级教师记为A6，则抽取2名教师的所有可能结果为{A1，A2}，{A1，A3}，{A1，A4}，{A1，A5}，{A1，A6}，{A2，A3}，{A2，A4}，{A2，A5}，{A2，A6}，{A3，A4}，{A3，A5}，{A3，A6}，{A4，A5}，{A4，A6}，{A5，A6}，共15种．

    从6名教师中抽取的2名教师均为初级教师(记为事件B)的所有可能结果为{A1，A2}，{A1，A3}，{A2，A3}，

    共3种．所以P(B)＝ .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥P﹣ABC中，PA⊥底面ABC，∠BAC=90°．点D，E，N分别为棱PA，PC，BC的中点，M是线段AD的中点，PA=AC=4，AB=2．

    （Ⅰ）求证：MN∥平面BDE；
    （Ⅱ）求二面角C﹣EM﹣N的正弦值；
    （Ⅲ）已知点H在棱PA上，且直线NH与直线BE所成角的余弦值为 ，求线段AH的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，平面平面，四边形为矩形，为的中点，为的中点.

    （1）求证：；

    （2）求证：平面.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某中学将100名高一新生分成水平相同的甲、乙两个“平行班”，每班50人．陈老师采用A，B两种不同的教学方式分别在甲、乙两个班级进行教改实验．为了解教学效果，期末考试后，陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计，作出茎叶图如图．记成绩不低于90分者为“成绩优秀”．

    （1）在乙班样本的20个个体中，从不低于86分的成绩中随机抽取2个，求抽出的2个均“成绩优秀”的概率；

    （2）由以上统计数据作出列联表，并判断能否在犯错误的概率不超过0.1的前提下认为：“成绩优秀”与教学方式有关．

    0.400

    0.250

    0.150

    0.100

    0.050

    0.025

    0.708

    1.323

    2.072

    2.706

    3.841

    5.024

    参考公式：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，平面，在直角梯形中，，，， 为线段 的中点

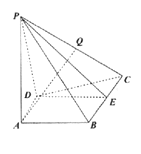
    （1）求证：平面平面

    （2）在线段 上是否存在点 ，使得平面 ?若存在，求出点 的位置；若不存在，请说明理由

    （3）若 是中点，，，，求三棱锥的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某研究机构对高三学生的记忆力和判断力进行统计分析，得下表数据：

    （1）请根据上表提供的数据，用相关系数说明与的线性相关程度；（结果保留小数点后两位，参考数据: ）

    （2）请根据上表提供的数据，用最小二乘法求出关于的线性回归方程；

    （3）试根据求出的线性回归方程，预测记忆力为9的同学的判断力．

    参考公式：，；相关系数；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）讨论函数的单调性；

    （2）若不等式在时恒成立，求实数的取值范围；

    （3）当时，证明： ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将3本相同的小说，2本相同的诗集全部分给4名同学，每名同学至少1本，则不同的分法有（ ）

    A. 24种 B. 28种 C. 32种 D. 36种

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某百货公司1～6月份的销售量与利润的统计数据如下表：

    月份

    1

    2

    3

    4

    5

    6

    销售量x（万件）

    10

    11

    13

    12

    8

    6

    利润y（万元）

    22

    25

    29

    26

    16

    12

    附：

    （1）根据2～5月份的统计数据，求出关于的回归直线方程

    （2）若由回归直线方程得到的估计数据与剩下的检验数据的误差均不超过万元，则认为得到的回归直线方程是理想的，试问所得回归直线方程是否理想？（参考公式：，）

    查看答案和解析>>

    同步练习册答案